Question

Question #6950a

Answer 1

Here's what I got.

Explanation:

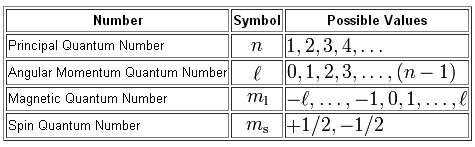
As you know, a full set of quantum numbers contains `4` values that we can use to describe the location and spin of an electron in an atom.

Your starting point here will be the electron configuration of a neutral silicon atom, which looks like this

`"Si: " 1s^2 2s^2 2p^6 color(blue)(3)s^2 color(blue)(3)p^2`

Now, by

the last electron of a silicon atom

I assume that you mean the electron that would be added last to the electron configuration of silicon.

The Aufbau Principle states that electrons fill empty orbitals in order of increasing energy levels. In your case, the highest energy level that holds electrons in a silicon atom will be the third energy level.

This means that the principal quantum number, `n`, of this electron will be

`ul(n = color(blue)(3))`

The angular momentum quantum number, `l`, tells you the energy subshell in which the electron is located. In this case, two subshells contain electrons on the third energy level of a silicon atom

• the `color(blue)(3)s` subshell `-> l = 0`
• the `color(blue)(3)p` subshell `-> l = 1`

The `p` subshell is actually higher in energy than the `s` subshell, which means that the two electrons added to the `color(blue)(3)p` subshell will be added last to the atom.

This means that you have

`ul(l = 1)`

The magnetic quantum number, `m_l`, tells you the exact orbital which holds the electron. For the `p` subshell, you have three possible orbitals

`l = 1 implies m_l = {-1, 0 ,1}`

By convention, these three values of the magnetic quantum number designate the following orbitals

• `m_l = -1 ->` the `p_x` orbital
• `m_l = color(white)(-)0 ->` the `p_z` orbital
• `m_l = color(white)(-)1 ->` the `p_y` orbital

Now, it's important to keep in mind that the two electrons will be added to separate `p` orbitals, as opposed to the same `3p` orbital `->` think Hund's Rule here.

In other words, and once again by convention, you can say that one of the two electrons will occupy the `3p_x` orbital and the other electron will occupy the `3p_z`.

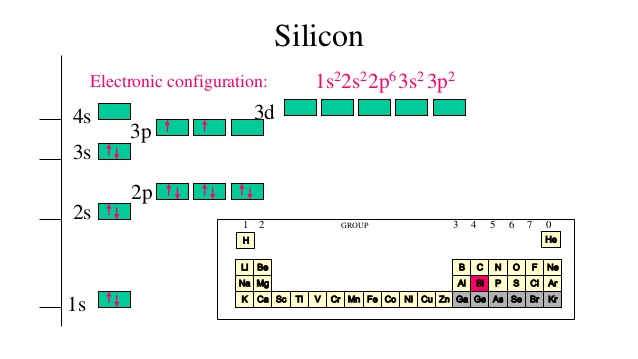
Therefore, these two electrons will have

`m_l = -1" "` and `" "m_l = 0`

Finally, the spin quantum number, `m_s`, tells you the spin of the electron.

By convention, electrons that are added to an empty orbital are assigned a positive spin, or `m_s = +1/2`. Both of these electrons will thus have

`m_s = +1/2`

Therefore, you can say that the two electrons added last to the electron configuration of a neutral silicon atom will have the following sets of quantum numbers

`n = 3, l=1, m_l = -1, m_s = +1/2`

This electrons is located on the third energy level, in the 3p subshell, in the `3p_x` orbital, and has spin-up

`n = 3, l=1, m_l = 0, m_s = +1/2`

This electrons is located on the third energy level, in the 3p subshell, in the `3p_z` orbital, and has spin-up

If you want to pick one electron as the one added last, go with the electron added to the `3p_z` orbital, since the electron located in the `3p_x` orbital will be added before the one located in the `3p_z` orbital.