Estimate the area under the curve #1/(x-1)^2# over the interval #[2,3]# with #n=4# using the trapezium rule?
1 Answer
Trapezium rule gives:
# int_2^3 \ 1/(x-1)^2 \ dx ~~ 0.51 # (2dp)
Explanation:
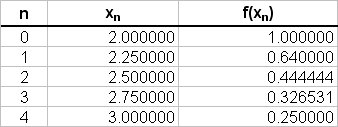
The values of
Using the trapezoidal rule:
# int_a^bydx ~~ h/2{(y_0+y_n)+2(y_1+y_2+...+y_(n-1))}#
We have:
# int_2^3 \ 1/(x-1)^2 \ dx #
# " " ~~ 0.25/2 { (1 + 0.25) + 2(0.64 + 0.444444 + 0.32653) } #
# " " = 0.125 { 1.25 + 2(1.410975) } #
# " " = 0.125 { 1.25 + 2.82195 } #
# " " = 0.125 { 4.07195 } #
# " " = 0.508993 #
Let's compare this to the exact value:
# int_2^3 \ 1/(x-1)^2 \ dx = [-1/(x-1)]_2^3 #
# " " = -(1/2-1) #
# " " = 0.5 #