Question

Question #4ab15

Answer 1

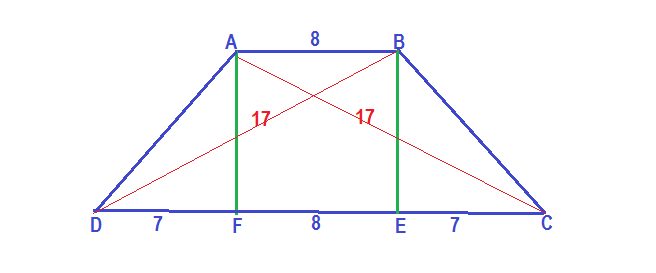
Given that ABCD is trapezium. It two parallel sides `AB = 8 and CD=22`. The diagonals `AC=BD=17`

`BE and AF` are perpendiculars drawn from B an A respectively.

The diagonals of the trapezium being equal it must be isosceles trapezium. So `AD=BC`

`DeltaADF~=DeltaBCE->DF=CE`

Now `AB =EF=8`

Again `CD =22`

`=>DF+EF+CE =22`

`=>2DF+8 =22`

`=>2DF =22-8=14`

`=>DF=7`

So `DE=DF+EF=7+8=15`

In `DeltaBDE,/_BED " is rt angle"`

So by Pythagorean theorem we have

`BE^2+DE^2=BD^2`

`=>BE^2+15^2=17^2`

`=>BE^2=17^2-15^2=64`

`=> BE= 8`

So area of trapezoid ABCD

`=1/2xx(AB+CD)xxBE=1/2xx(8+22)xx8=120` squnit