Question

Question #30d1d

Answer 1

Consider an object which rests on a plain surface and is being pushed with a force towards right as shown in the figure. In the event of no motion of the object we see that:
Four forces acting on the object are in equilibrium.

`"Force of Gravity "darr="Normal Force "uarr`

and

`"Force of Friction "larr="Applied Force "rarr`

We know that friction force is the force exerted by a surface as an object moves or makes an attempt to move across it.

There are two types of friction forces - static and sliding friction forces. The friction force often opposes the motion of an object. Friction depends upon the nature of the two surfaces in contact and upon the degree to which they are pressed together. The maximum amount of friction force that a surface can exert upon an object can be calculated using the formula below:

`F_"friction" = mu cdot F_"normal"`
where `mu` is coefficient of friction.
`=> mu =F_"friction"/ F_"normal"`

Coefficient of friction is of two kinds
A. For surfaces which are stationary relative to each other

`mu =mu_s`
Here `mu _s`, is called the coefficient of static friction.

B. For surfaces which are in relative motion

`mu =mu _k`
Here `mu _k` is called the coefficient of kinetic friction

For an object which is just about to slide down an inclined plane of angle `theta` as shown in the figure below,

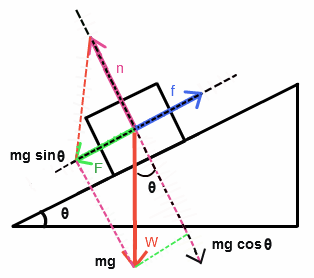
we define static friction in terms of the maximum angle before which the object begins sliding. This is called the angle of friction.
It is defined as:

`tan ⁡ theta = mu_s`

In the figure above
`F_"friction"` is shown as `f` in blue
and `F_"normal"` is shown as `n` in pink