Question #0c91a
1 Answer
In order to explain the discrete nature of radiation caused by an excited atom Bohr postulated quantisation of electron orbits in an atom.
According to his hypothesis electrons are allowed only to rotate around the nucleus in those circular orbits where the angular momentum of rotation of electron is integral multiple of
I.e.
where
An interpretation of Bohr's equation is obtained later by the theory of matter wave put forwarded by de Broglie.
According to de Broglie the wave length (
The movement of an electron in a circular orbit of radius
Combining [2] and [3] we get
Bohr's equation[1}
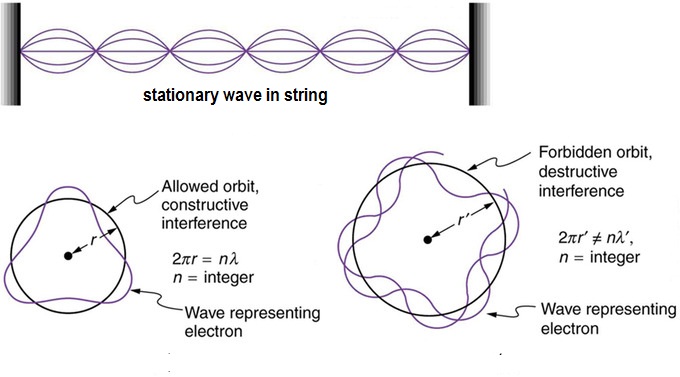
So according to equation [3} the number of electron waves in an orbit is the principal quantum number (n) of the orbit which is related to the azimuthal quantum number (l)as follows
Again the magnetic quantum number
Here the maximum value of
So
Hence the number of waves should be

