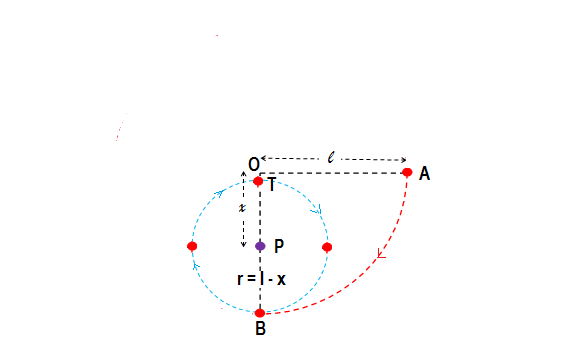
Let a mass of #m# attached to the end of a string of length #l# which is tied to a fixed point #O# be released from the initial horizontal position of the string #OA#.
When it reaches at the bottom position #B# of the initial circular path, let the velocity of the mass at #B# be # v_B#.
This velocity is gained by the mass at position B due to decrease in PE for the fall of height #l# from its initial static position A .
So we have by conservation of energy #1/2mv_B^2=mgl#
#=>v_B^2=2gl......[1]#
When the mass reaches at B the string hits the peg #P#, fixed below the point #O# at a distance #x # from #O# and mass begins to move in the vertical circle of radius #PB=r=(l-x)# centering the peg #P#
Let T represents the top position in the new vertical circular path and # v_T# represents the velocity at this position T.
Considering conservation of energy at #B and T# we can write
#KE" at T"#
#= KE" atB" -"gain of PE due to lift of height 2r (B to T) "#
#=>1/2mv_T^2=1/2mv_B^2-2mgr#
#=>v_T^2=v_B^2-4gr.......[2]#
The mass will complete the circle, if the string doesn't slack at the highest point. The minimum centripetal force required for this will be provided by the weight of the moving mass #m# i.e. #mg#
So we can write
#(m(v_T^2)_"min")/r =mg#
#=>(v_T)_min=sqrt(gr).......[3]#
Inserting this value in equation [2] we can get the minimum required velocity #(v_B)_"min"# of the mass at position #B #
#=>v_T^2=v_B^2-4gr#
#=>(v_T^2)_ min=(v_B^2)_"min"-4gr#
#=>(v_B^2)_"min"=(sqrt(gr))^2+4gr#
#=>(v_B^2)_"min"=5gr#
This can also be written as
#=>v_B^2>=5gr.....[4]#
So this is the required condition to make the mass describe the complete the circle of radius #r=(l-x)#
Hence by relations [1] and [4] we get
#=>2gl>=5gr#
#=>2l>=5(l-x)#
#=>5x>=5l-2l#
#=>x>=(3l)/5#, which is option (1)


