Question #5dc62
1 Answer
Bismuth-214.
Explanation:
All you really need to use in order to answer this question is a Periodic Table and the fact that when a radioactive nuclide undergoes alpha decay
- its atomic number decreases by two,
#color(green)(Z - 2)# - its mass number decreases by four,
#color(blue)(A - 4)#
This is the case because when a radioactive nuclide undergoes alpha decay, its emits an alpha particle, which is essentially the nucleus of a helium-4 atom.
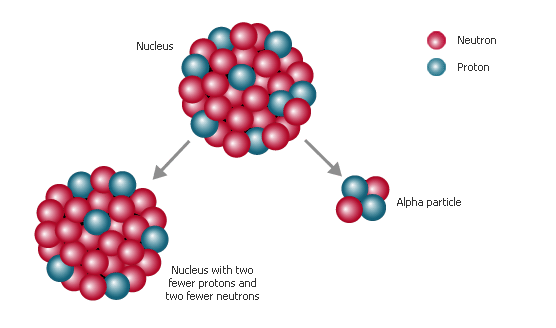
So, grab a Periodic Table and look for astatine,
Astatine has an atomic number equal to
#""_(color(white)(1)color(green)(85))^color(blue)(218)"At"#
Since an alpha particle contains
#""_ (color(white)(1)color(green)(85))^color(blue)(218)"At" -> ""_ color(green)(Z)^color(blue)(A)"?" + ""_ color(green)(2)^color(blue)(4)alpha#
Your goal here is to find the identity of the unknown nuclide, which we labeled as "
As you know, mass and charge must be conserved in a nuclear reaction. This implies that the total mass number and the total atomic number must be equal on both sides of the equation.
You can thus say that
conservation of mass
# ->" "color(blue)(218 = A + 4)# conservation of charge
# -> " "color(green)(85 = Z + 2)#
This will get you
#color(blue)(A = 218 - 4 = 214)" "# and#" "color(green)(Z = 85 - 2 = 83)#
Check the Periodic Table for the element that has an atomic number equal to
#""_ color(green)(Z)^color(blue)(A)"?" = ""_ (color(white)(1)color(green)(83))^color(blue)(214)"Bi"#
Therefore, you can say that the alpha decay of astatine-218 will produce bismuth-214, or
The complete nuclear equation will be
#""_ (color(white)(1)color(green)(85))^color(blue)(218)"At" -> ""_ (color(white)(1)color(green)(83))^color(blue)(214)"Bi" + ""_ color(green)(2)^color(blue)(4)alpha#

