I have assumed that the equation is #f(x)=kx * (1-x)#
and you want to know the effect of varying the value of #k#.
Here is a graph with sample values of #k# (I did not limit it to the interval #[0.1]# but you can ignore everything below the X-axis).
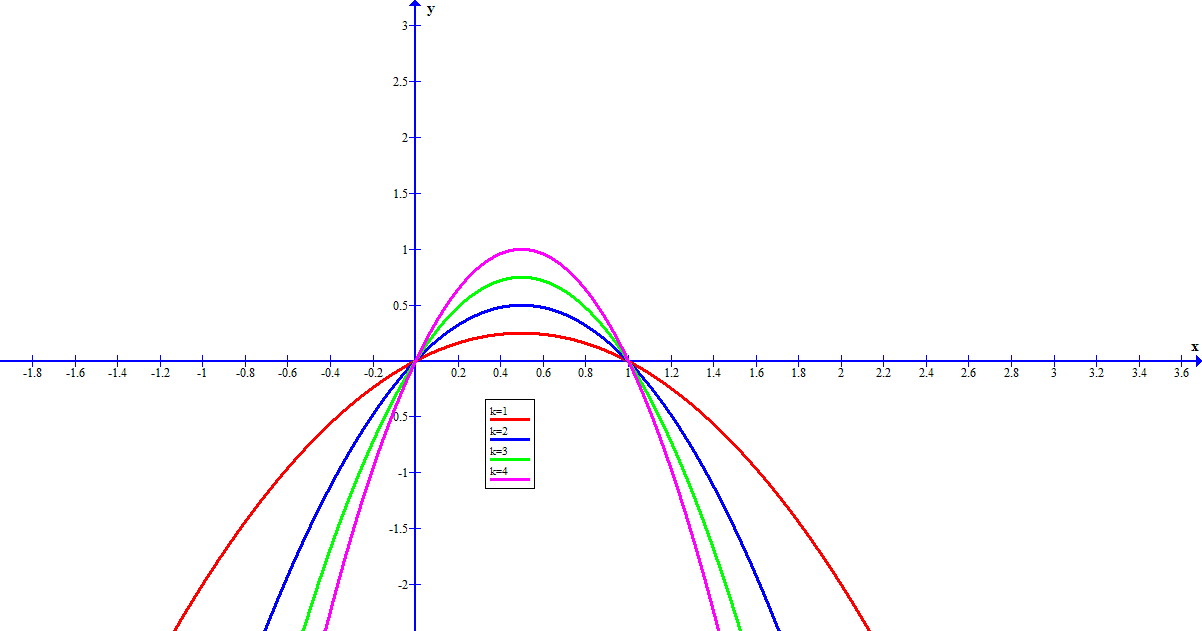
As you can see as #k# increases in value the vertex rises and the sides get "squeezed" in.
For the interval #[0,1]# you are probably more interested in the vertex.
If #f(x)=k * x * (1-x)#
#color(white)("XXX")=kx-kx^2#
#color(white)("XXX")=(-k)(x^2-x)#
#color(white)("XXX")=(-k)(x^2-x+1/4)+k/4#
#color(white)("XXX")=(-k)(x-1/2)^2+k/4#
which is the vertex form of a parabola with vertex at #(1/2,color(red)(k/4))#
So we can see that the #x# coordinate of the parabola stays constant but the #y# coordinate varies as #1/4# of the value of #k# with changing values of #k#.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Hope this is in some way related to what you were looking for.

