Question #4ee02

Question

1331 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-04-01T17:07:01

It can be solved like this:

1.

This is not a well worded question since the rate of the reaction is not constant. I will assume they are asking for the average rate after 40 min.

Average rate = loss of sulfur / time

Average rate = #sf((0.8-0.4)/(40)= 0.01color(white)(x)"min"^-1)#

2.

There are several methods you could use to show this. I will use "The Integral Method".

#sf(Ararr"products")#

For a 1st order reaction we have:

#sf("Rate"=k[A]^1)#

Where k is the rate constant.

This can be expressed in terms of the rate of disappearance of A :

#sf(-(d[A])/(dt)=k.dt)#

Rearranging and applying integration between 0 and t gives:

#sf(int_([A]_0)^([A]_t)(d[A])/([A])=-kint_0^tdt)#

This gives:

#sf(ln[A]_(t)-ln[A]_0=-kt)#

#:.##sf(ln[A]_t=ln[A]_0-kt)#

This means that if the reaction is 1st order then a plot of #sf(ln[A]_t)# against t should be a straight line of the form #sf(y=mx+c)#

The gradient of the line will be equal to -k.

Excel is a useful tool to do this (other spreadsheet programmes are available) . Here's what I got:

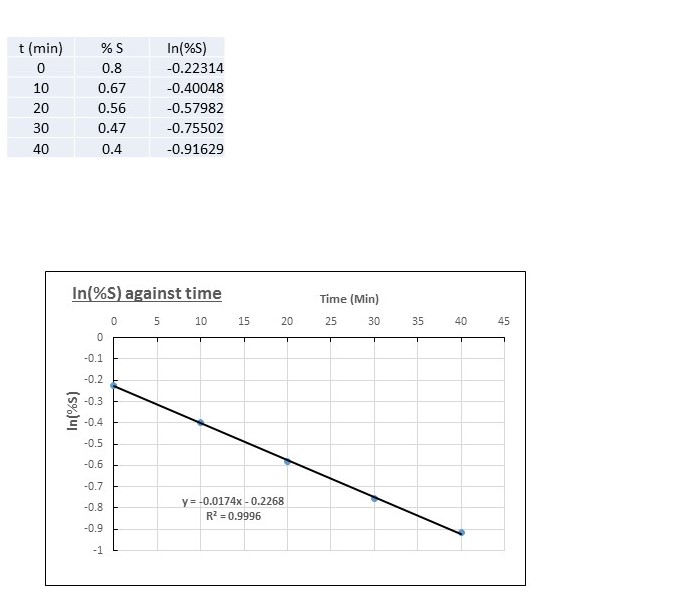
MF Docs

The straight line confirms that the reaction is 1st order.

Since #sf(R^2=0.9996)# this means the correlation coefficient #sf(R=sqrt(0.9996)=0.9997)#. This indicates an almost perfect fit.

The equation of the line has been added by the programme for you:

#sf(y=-0.0174x-0.2268)#

This tells us that #sf(-k=-0.0174color(white)(x)"min"^(-1))#

#:.##sf(k=0.0174color(white)(x)"min"^-1)#

3.

We now have the rate equation for the reaction:

Rate = #sf(kxx%S)#

At the 30th minute the %S = 0.47

#:.##sf("Rate"=0.0174 xx 0.47=0.0082color(white)(x)"min"^(-1))#