Question #c7286
1 Answer
In a 1st order reaction, the rate is directly proportional to the concentration of the reactants.
Explanation:
Hence, the rate is fast at the beginning.
As the reactants get used up the reaction goes slower and slower and slower
and …
We can see this happening in the first order plot shown below.
The blue curve is a plot of a first order reaction in which
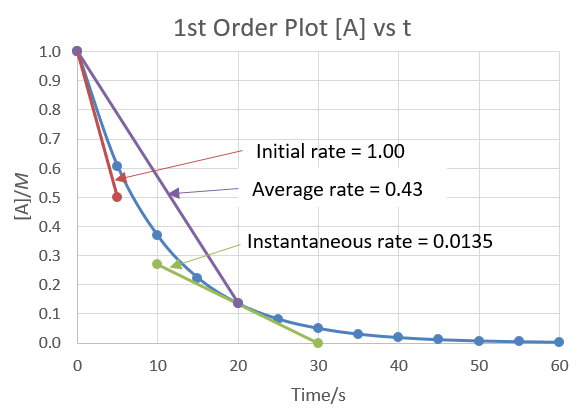
The instantaneous rate at a given time
The slope of the line is a measure of the rate (
Instantaneous rate at
The
Since the reaction has just started, [A] is at its maximum and the rate is fastest
(
Instantaneous rate at
At
Average rate
The average rate from 0 s to 20 s (shown by the
We see that the slope of this line (

