Question

Find the area bounded by `x = -y^2` and `y = x+2` using a double integral?

(portions of this question have been edited or deleted!)

Answer 1

Bounded Area = `9/2`

Explanation:

Based on the sketch. we are looking for a double integral solution to calculate the area bounded by the curves:

`x = -y^2`
`y = x+2 = > x=y-2`

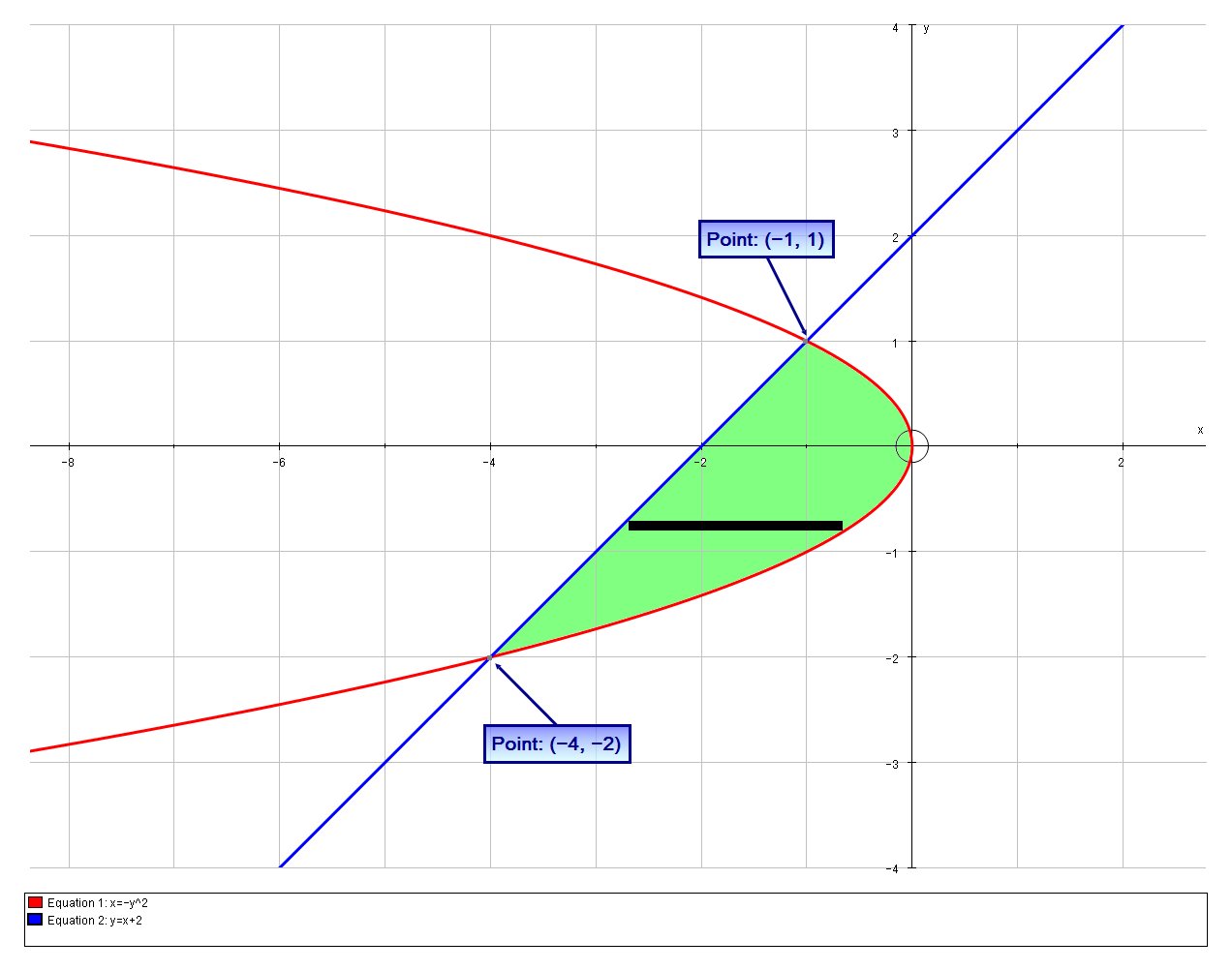
The points of intersection are the solution of the equation:

`x = -(x+2)^2`
`:. x = -(x^2+4x+4)`
# :. x^2+5x+4 = 0 # :. (x+1)(x+4) = 0# # :. x=-1, -4#

The corresponding `y`-coordinates are:

`x=-1 => y=1`
`x=-4 => y=-2`

Giving the coordinates `(-1,1)` and `(-4,-2)`

If in the above diagram we look at an infinitesimally thin horizontal strip (in black) then the limits for `x` and `y` are:

`x` varies from `y-2` to `-y^2`
`y` varies from `-2` to `1`

And so we can represent the bounded are by the following double integral:

`A = int int_R dA`
`\ \ \ = int_-2^1 \ int_(y-2)^(-y^2) \ dx \ dy`

We can calculate the inner integral:

`int_(y-2)^(-y^2) \ dx = [x]_(y-2)^(-y^2)`

`" " = (-y^2) - (y-2)`
`" " = -y^2 - y+2`
`" " = -(y^2 + y-2)`

And so:

`A = int_-2^1 \ int_(y-2)^(-y^2) \ dx \ dy`
`\ \ \ = int_-2^1 -(y^2 + y-2) \ dy`
`\ \ \ = - int_-2^1 y^2 + y-2 \ dy`
`\ \ \ = - [ y^3/3 + y^2/2-2y ]_-2^1`
`\ \ \ = - {(1/3+1/2-2)-(-8/3+2+4)}`
`\ \ \ = - {(-7/6)-(10/3)}`
`\ \ \ = 9/2`