Question

`220` cars are rented at `$30` per day and for each dollar increase, `5` fewer cars are rented. What is the maximum possible income and the rent at which this maximizes?

Answer 1

Maximum income of `$6,845` is at a rent of `$37` per day.

Explanation:

Let number of cars rented at a rate of `r` dollars per day be `n`. Hence revenue would be `R=$nr`.

As `220` cars are rented at `$30` per day and for each dollar increase, `5` fewer cars are rented

at `r` dollars number of cars rented (i.e. `30-r` dollars less than `$30`), cars rented would be `300+5(30-r)` or

`n=220+5(30-r)` and revenue is given by `R=r(220+5(30-r))`

or `R=r(370-5r)=370r-5r^2`

and this will maximized when `(dR)/(dr)=0`

as `(dR)/(dr)=370-10r=0` i.e. `r=37`

Hence, revenue is maximized when rate is `$37` per day. At this rate number of cars hired is `220+5(30-37)=220-35=185`

and revenue is `$6,845`

Answer 2

TR is maximum when 185 cars are rented out.

Revenue maximising daily rent = 37

Maximum Revenue `=6845`

Explanation:

We can form a demand curve using the given information.
Daily Rent is measured along the Y - axis. We shall have Daily Rate as Price and symbolize it as `p`. It is independent variable in our analysis.

Number of cars is measured along the X - axis. Let us symbolize it as `q`. It is dependent variable in our analysis.

We shall develop the AR function [Demand function]

`q_1=220`
`p_1=30`
`q_2=215`
`p_2=31`

`(p-p_1)=(p_2-p_1)/(q_2-q_1)(q-q_1)`

`p-30=(31-30)/(215-220)(q-220)`

`p-30=-1/5(q-220)`

`p-30=-1/5q+44`

`p=-1/5q+44+30`

`p=-1/5q+74` [AR function]

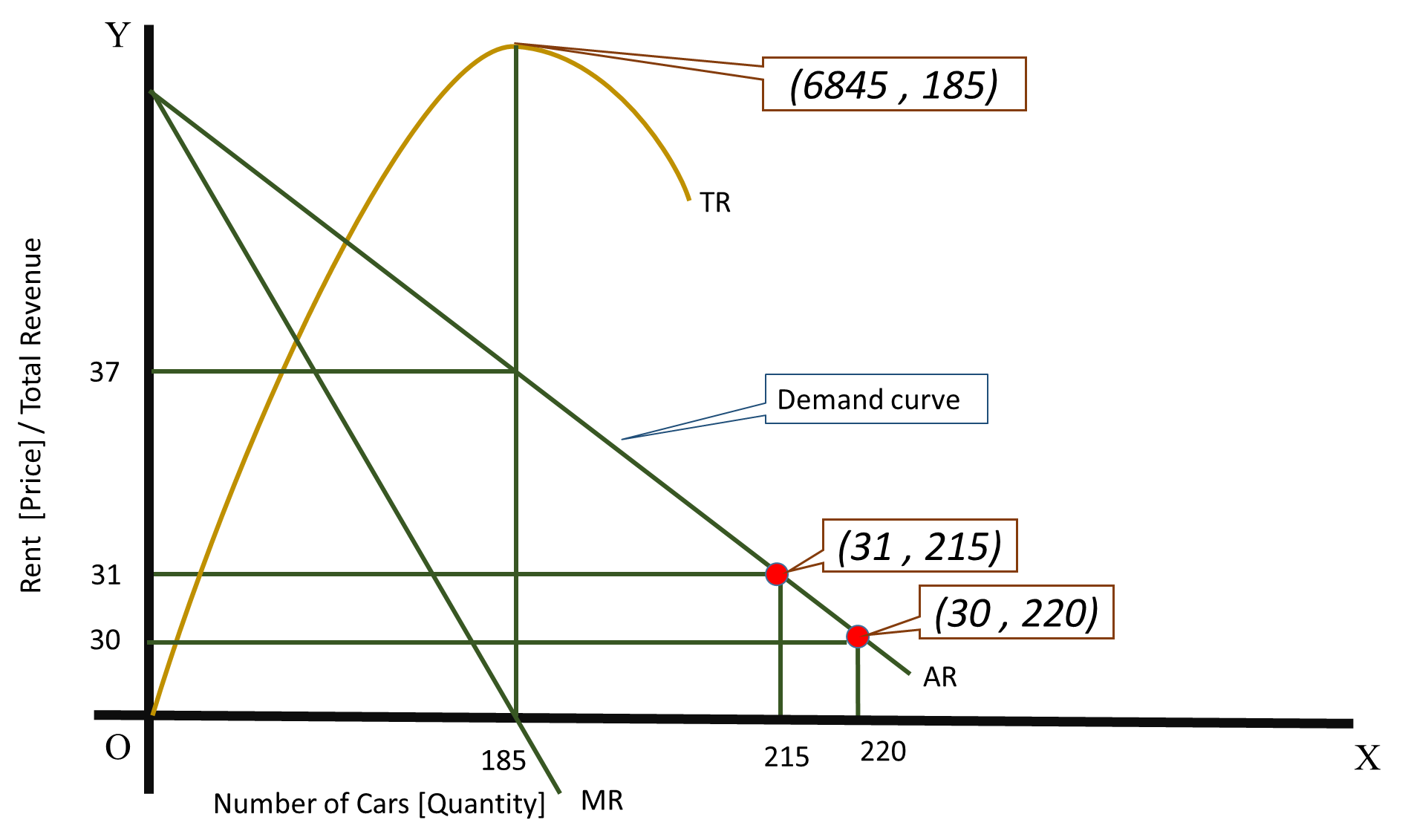
Since AR curve is downward sloping and linear, the slope of the MR curve is double the slope of AR curve. Using this piece of information let us form the MR function.

MR`=[(-1/5)xx2]x+74`

MR`=-2/5x+74`

Total Revenue is Maximum when MR = 0.

`-2/5x+74=0`

`x=-74xx(-5/2)=370/2=185`

TR is maximum when 185 cars are rented out.

To find the price, substitute `q=185 in the Ar function`

AR `=-1/5x+74`
AR `=-1/5 xx 185+74=-37+74=37`

Revenue maximising daily rent = 37

Maximum Revenue = Number of cars `xx` Daily rent

Maximum Revenue =185 `xx` 37 `=6845`