Question

a) Show that the formula for the surface area of a sphere with radius `r` is `4pir^2`. b) If a portion of the sphere is removed to form a spherical cap of height `h` then then show the curved surface area is `2pihr^2`?

a) Show that the formula for the surface area of a sphere with radius `r` is `4pir^2`.

b) If a portion of the sphere is removed to form a spherical cap of height `h` then then show the curved surface area is `2pihr^2`

Answer 1

A = int dA

Explanation:

An area element on a sphere has constant radius r, and two angles. One is longitude `phi`, which varies from `0` to `2pi`. The other one is the angle with the vertical. To avoid counting twice, that angle only varies between `0` and `pi`.

So the area element is `dA = r d theta r sin theta d phi = r^2 sin theta d theta d phi`
Integrated over the whole sphere gives
`A = int_0^pi sin theta d theta int_0^(2pi) dphi r^2 = -cos(theta)|_0^(pi) 2 pi r^2 = 4 pi r^2`

In part b, `cos(theta)` varies between `a/r` and `b/r` which is such that `b-a=h`
Then `A= cos theta|_b^a 2pi r^2 = (b/r - a/r) 2 pi r^2 = (h/r) 2pi r^2 = 2 pi r h`

Note: Every derivation I found of this result uses cylindrical coordinates and is far more involved than this one. Can someone else check?

Answer 2

a) `A = 4pir^2`
b) `A = 2pihr^2`

Explanation:

It is easier to use Spherical Coordinates, rather than Cylindrical or rectangular coordinates. This solution looks long because I have broken down every step, but it can be computer in just a few lines of calculation

With spherical coordinates, we can define a sphere of radius `r` by all coordinate points where `0 le phi le pi` (Where `phi` is the angle measured down from the positive `z`-axis), and `0 le theta le 2pi` (just the same as it would be polar coordinates), and `rho=r`).

The Jacobian for Spherical Coordinates is given by `J=rho^2 sin phi`

And so we can calculate the surface area of a sphere of radius `r` using a double integral:

`A = int int_R \ \ dS \ \ \`

where `R={(x,y,z) in RR^3 | x^2+y^2+z^2 = r^2 }`

`:. A = int_0^pi \ int_0^(2pi) \ r^2 sin phi \ d theta \ d phi`

If we look at the inner integral we have:

`int_0^(2pi) \ r^2 sin phi \ d theta = r^2sin phi \ int_0^(2pi) \ d theta`
`" " = r^2sin phi [ \ theta \ ]_0^(2pi)`
`" " = (r^2sin phi) (2pi-0)`
`" " = 2pir^2 sin phi`

So our integral becomes:

`A = int_0^pi \ 2pir^2 sin phi \ d phi`
`\ \ \ = -2pir^2 { cos phi ]_0^pi`
`\ \ \ = -2pir^2 (cospi-cos0)`
`\ \ \ = -2pir^2 (-1-1)`
`\ \ \ = -2pir^2 (-2)`
`\ \ \ = 4pir^2 \ \ \` QED

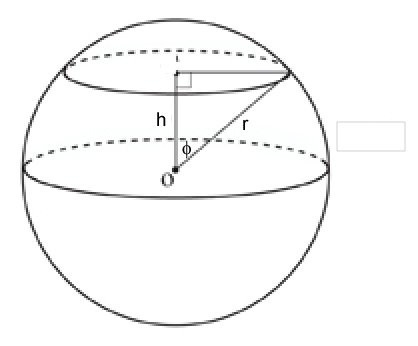
For the area of the portion of a sphere we have a similar set-up:

By trigonometry `cos phi = h/r => phi = arccos(h/r)`, and so we must restrict `phi` to `arccos(h/r) le phi le pi/2`, which gives us:

`A = int_arccos(h/r)^(pi/2) \ int_0^(2pi) \ r^2 sin phi \ d theta \ d phi`
`\ \ \ = int_arccos(h/r)^(pi/2) \ (r^2sin phi)(2pi-0) \ d phi`
`\ \ \ = int_arccos(h/r)^(pi/2) \ 2pir^2sin phi \ d phi`
`\ \ \ = -2pir^2[cosphi]_arccos(h/r)^(pi/2)`
`\ \ \ = -2pir^2(cos(pi/2)-cos(arccos(h/r)))`
`\ \ \ = -2pir^2(0-h/r)`
`\ \ \ = -2pir^2(-h/r)`
`\ \ \ = 2pihr^2 \ \ \` QED