Question #8d6ed
1 Answer
Graham's law of effusion states that the rate of effusion of a gas is inversely proportional to the square root of the mass of its particles.
If we have two gases, we can show that their relative rates of effusion (and diffusion) are given by the formula
#color(blue)(bar(ul(|color(white)(a/a)r_2/r_1 = sqrt(M_1/M_2)color(white)(a/a)|)))" "#
where
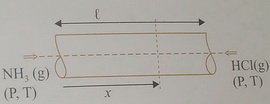
Let gas 1 be
Then
The distances traveled in a given time are proportional to the speeds (
Also,

