Question

Are angular nodes necessarily planes?

Answer 1

No, angular nodes can be nodal planes, but they can also be conical nodes. Angular nodes are more general, and nodal planes are an example.

Angular nodes are determined by finding what `l` corresponds to the orbital you are looking at.

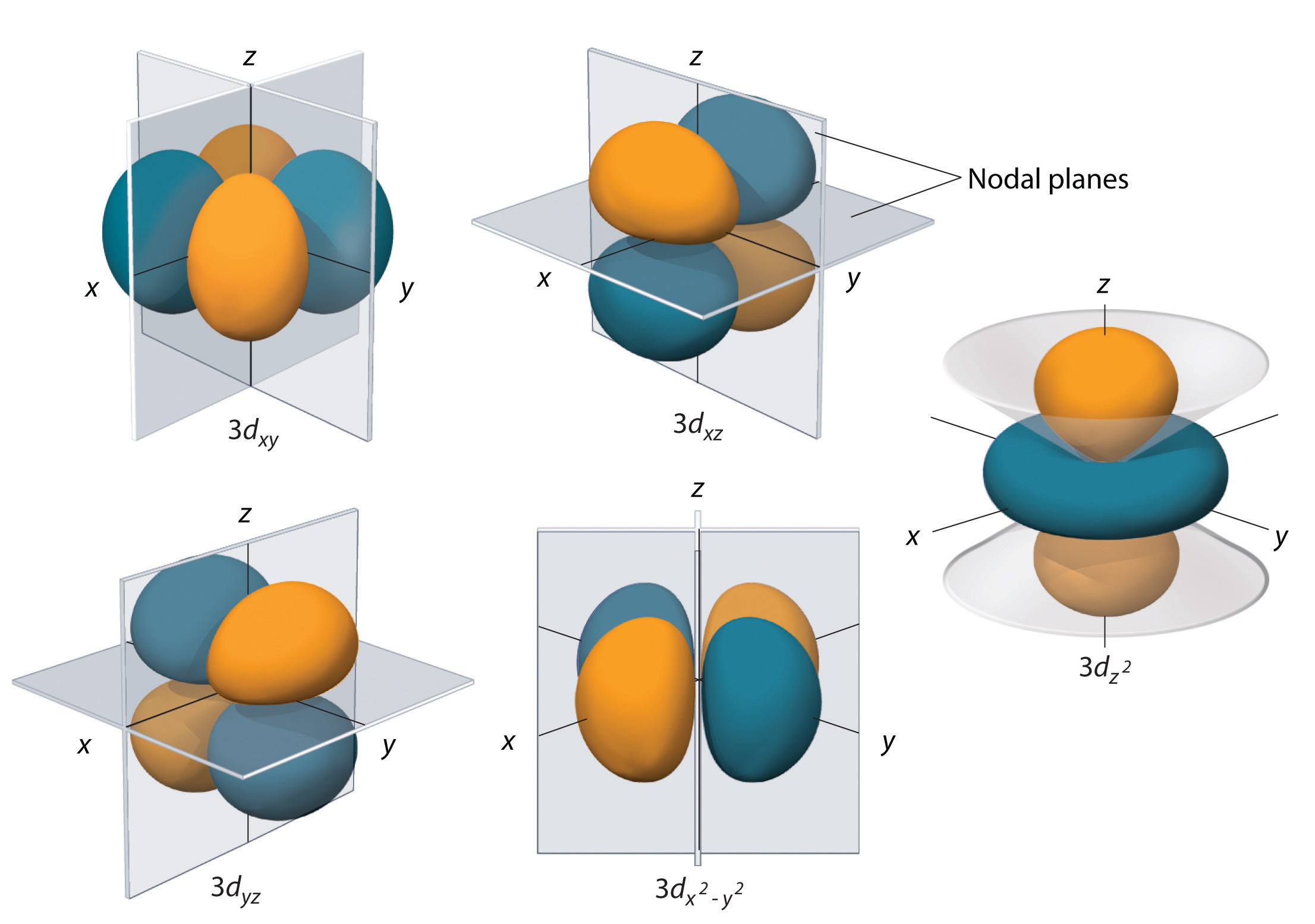https://saylordotorg.github.io/

For example, a `3d` orbital has `l = 2`, so it has two angular nodes. These happen to usually be nodal planes. For a `3d_(xy)` orbital, these are the `xz` and `yz` planes.

However, for the `3d_(z^2)` orbital, the two angular nodes correspond to the two conical nodes: the top half and the bottom half (these are at around `54.74^@` from the `z` axis).