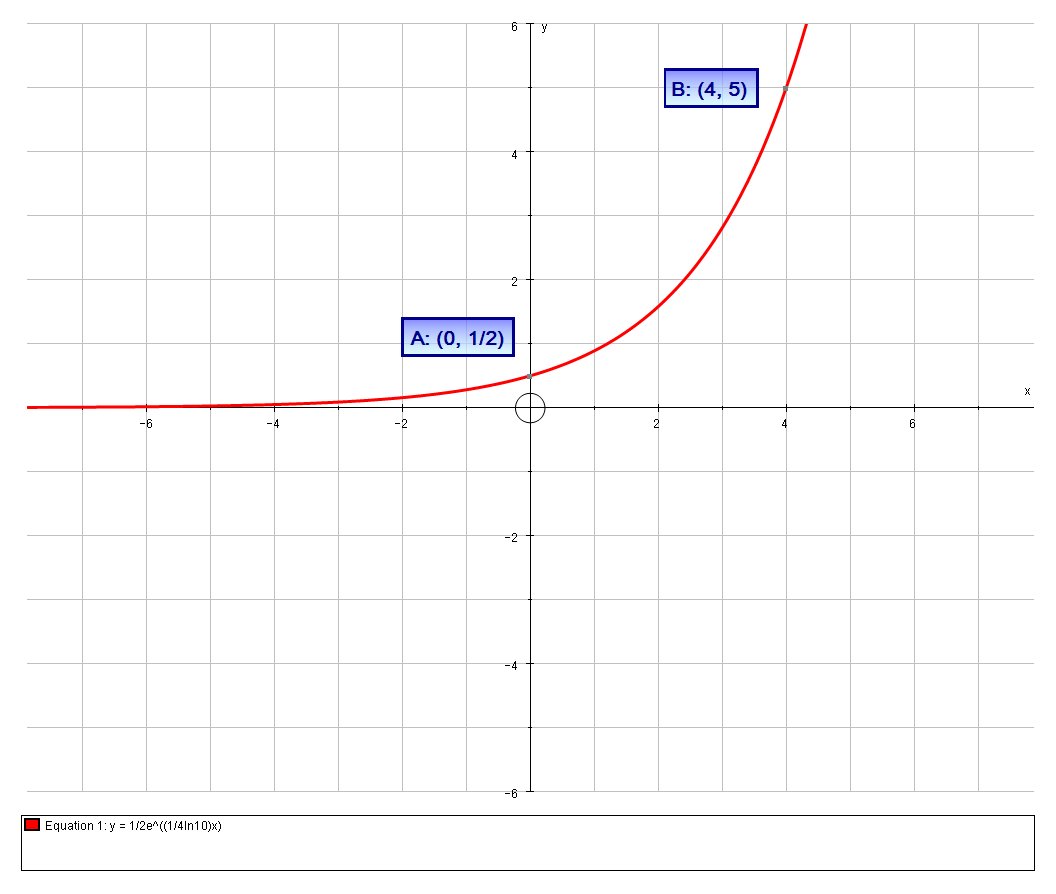
A mathematical model has an equation #y = ae^(bx)# and this curve passes through the points # A(0,1/2)# and #B(4,5) #. Find a and b?

Question

1199 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-09-18T19:25:50

#a = 1/2# and #1/4ln10 #

With these results we have:

# y = 1/2e^((1/4ln10)x) #

We have:

# y = ae^(bx) #

as a model. And we have two data points:

# A(0,1/2)# and #B(4,5) #

Using #A# we have:

# 1/2 = ae^(0) -> a = 1/2#

Using #B# we have:

# 5 = 1/2e^(b4) => e^(4b) = 10#
# :. 4b = ln10 #
# :. b = 1/4ln10 #

With these results we have:

# y = 1/2e^((1/4ln10)x) #

Which we can see graphically:

Steve M