Question

For the reaction `2A + B -> 3C`, if the rate of disappearance of `B` is `"0.30 mol/L"cdot"s"`, how do you set up a calculation to determine the rate of disappearance of `A` and appearance of `C`?

Answer 1

For

`2A + B -> 3C`,

knowing that the rate of disappearance of B is `"0.30 mol/L"cdot"s"`, i.e.

`(Delta[B])/(Deltat) = -"0.30 M/s"`,

we just have to check the stoichiometry of the problem. Note that the overall rate of reaction is therefore `+"0.30 M/s"`.

Since twice as much `A` reacts with one equivalent of `B`, its rate of disappearance is twice the rate of `B` (think of it as `A` having to react twice as fast as `B` in order to "keep up" with `B`).

Therefore:

`-1/2(Delta[A])/(Deltat) = -(Delta[B])/(Deltat)`

Similarly, since three equivalents of `C` are produced for every one equivalent of `B`, it must get produced three times as quickly in order to get produced in the same interval of time.

`color(blue)(-1/2(Delta[A])/(Deltat) = -(Delta[B])/(Deltat) = 1/3(Delta[C])/(Deltat))`

Knowing that, you can calculate the rate of disappearance of `A` and appearance of `C`.

---

Even reactions with large negative `DeltaG^@` at `25^@ "C"` and `"1 atm"` have a hard time occurring at that temperature and pressure simply because they're slow.

The activation energy is high for such reactions, and it is difficult for the molecules to find the opportunity to overcome it. They are simply colliding until a large enough fraction of the molecules have sufficient energy to overcome the reaction barrier.

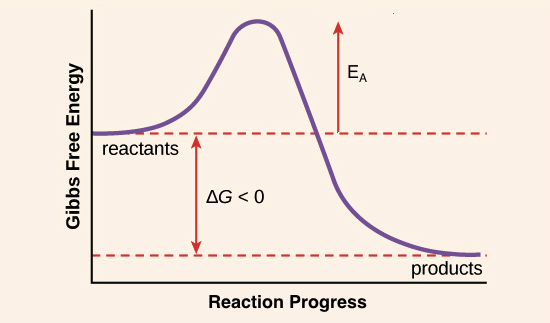
Until enough of them do, the reaction does not occur.