The point #P# lies on the #y#-axis and the point #Q# lies on the #y#-axis. A triangle is formed by connecting the origin #O# to #P# and #Q#, If #PQ=23# then prove that the maximum area occurs when when #OP=OQ#?
2 Answers
Let us start with a picture describing the problem:
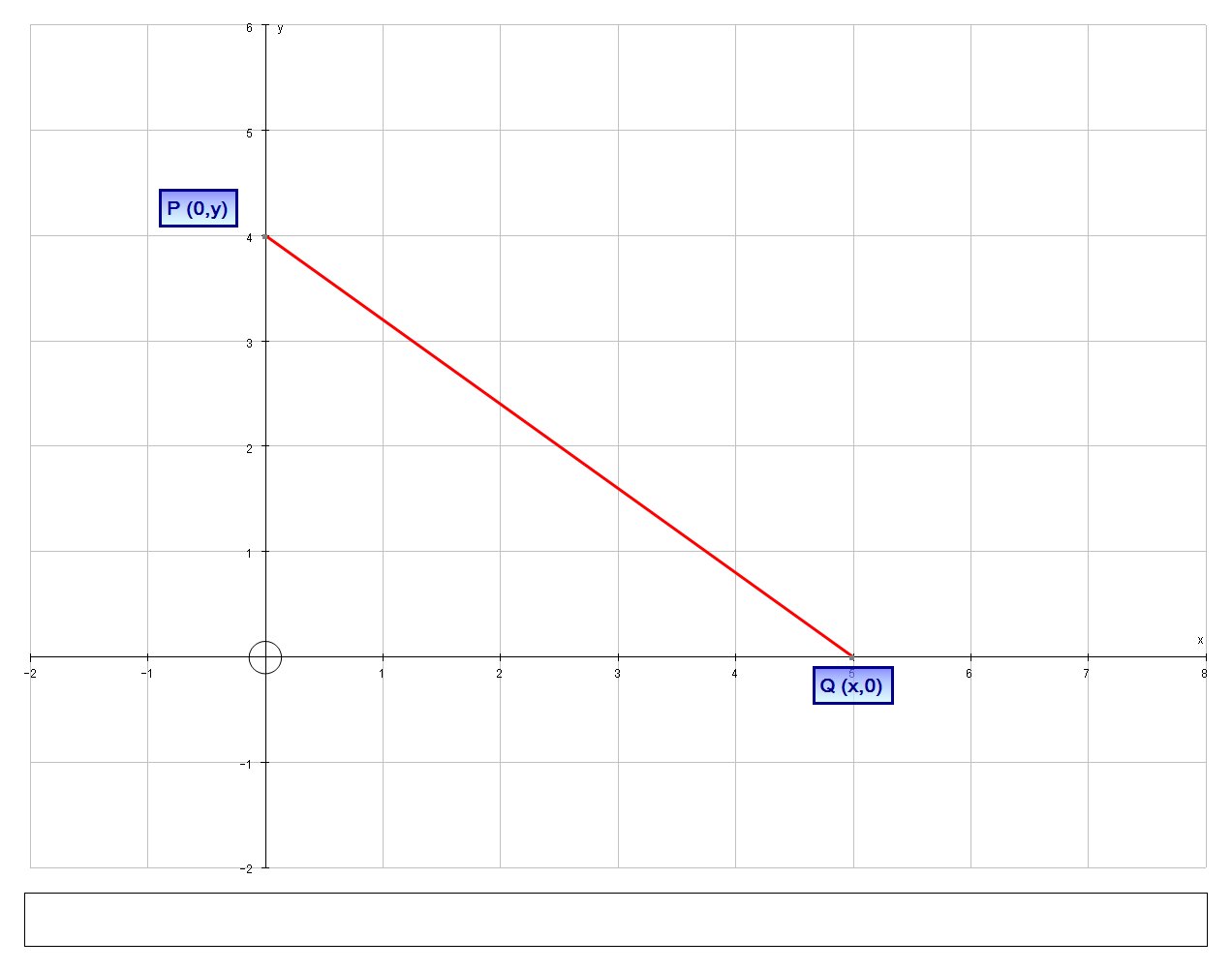
Our aim is find the area,
Let us set up the following variables:
# { (y, y"-Coordinate of the point P"), (x, x"-Coordinate of the point Q"),(A, "Area enclosed by the triangle OPQ") :} #
With all variables being positive. We are given that
# \ \ \ PQ^2 = AP^2+OQ^2 #
# :. 23^2 = y^2+x^2 #
# :. x^2+y^2 = 529 => y = sqrt(529-x^2) .... (star) #
And the Area ,
# A = 1/2(x)(y) #
# \ \ = 1/2xsqrt(529-x^2) #
Now this is where a little common sense can make life easier. We could use this function and find
Instead we can observe that a maximum in
# A = 1/2xsqrt(529-x^2) => 2A = xsqrt(529-x^2) #
so instead let us look at the function:
# Phi = (2A)^2 #
# \ \ \ = (xsqrt(529-x^2))^2 #
# \ \ \ = x^2(529-x^2) #
# \ \ \ = 529x^2-x^4 #
Then differentiating wrt
# (dPhi)/dx = 1058x-4x^3 #
At a min/max this derivative will be zero; thus:
# (dPhi)/dx = 0 => 1058x-4x^3 = 0#
# :. x(1058-4x^2) = 0#
# :. x = 0, 4x^2=1058 #
# :. x = 0, x^2=529/2 #
# :. x = 0, (23sqrt(2))/2 #
We can clearly eliminate
When
# y = sqrt(529-x^2) #
# \ \ = sqrt(529-529/2) #
# \ \ = sqrt(529/2) #
# \ \ = (23sqrt(2))/2 #
Thus the critical point correspond to
We should really validate that this critical point corresponds to a maximum., Given the earlier alternative answer
Differentiating our earlier result we have:
# \ \ \ \ \ \ (dPhi)/dx = 1058x-4x^3 #
# :. (d^2Phi)/dx^2 = 1058-12x^2 #
And with
# (d^2Phi)/dx^2 = 1058-12*529/2 #
# " " = -2116 #
# " " lt 0 => # maximum
Hence the maximum area enclosed by
The triangle formed by the points
Because the hypotenuse of this triangle has length
so that:
The area of such triangle is:
The function
and evaluating the derivative:
and then:
The maximum area is:


