Question #c3e59
2 Answers
B.
Explanation:
A.
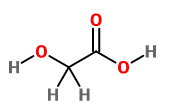
This compound has 1
B.
Ethanol
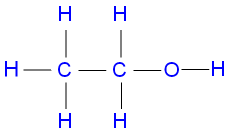
This compound has 1
C.

This compound contains 1
D.
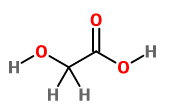
This compound contains 1
Explanation:
We can use the following formula to determine the number of covalent bonds in a molecule.
where
and
A) For compound
which consists of 2C ,2O and 6H ,we have
So
B) For compound
which consists of 2C ,1O and 6H ,we have
So
C) For compound
which consists of 2C ,4O and 2H ,we have
So
D) For compound
which consists of 2C ,3O and 4H ,we have
So


