Question

Which lanthanides are exceptions to the Aufbau principle?

Answer 1

See here for a fuller explanation on the lanthanides and actinides.

The order by atomic number is down the first column, and then down the second column. In `color(red)("red")` are the 'Aufbau exceptions'.

`color(white)([(color(red)(La),(color(red)([Xe] 6s^2 5d^1)),color(black)(Tb),(color(black)([Xe] 6s^2 4f^9))),(color(red)(Ce),(color(red)([Xe] 6s^2 4f^1 5d^1)),color(black)(Dy),(color(black)([Xe] 6s^2 4f^10))),(color(black)(Pr),(color(black)([Xe] 6s^2 4f^3)),color(black)(Ho),(color(black)([Xe] 6s^2 4f^11))),(color(black)(Nd),(color(black)([Xe] 6s^2 4f^4)),color(black)(Er),(color(black)([Xe] 6s^2 4f^12))),(color(black)(Pm),(color(black)([Xe] 6s^2 4f^5)),color(black)(Tm),(color(black)([Xe] 6s^2 4f^13))),(color(black)(Sm),(color(black)([Xe] 6s^2 4f^6)),color(black)(Yb),(color(black)([Xe] 6s^2 4f^14))),(color(black)(Eu),(color(black)([Xe] 6s^2 4f^7)),color(black)(Lu),(color(black)([Xe] 6s^2 4f^14 5d^1))),(color(red)(Gd),(color(red)([Xe] 6s^2 4f^7 5d^1)),"","")])`

Generally the electron configuration exceptions occur

• early in the lanthanide series (lanthanum, cerium)
• after filling the `4f` orbitals halfway (gadolinium).

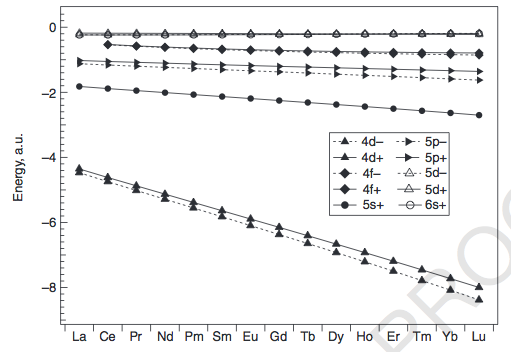
In general, it has to do with the closeness in energy of the `4f`, `5d`, and `6s` orbitals. The `5d` and `6s` are nearly the same energy across the entire lanthanide row, and the `4f` is fairly close in energy for the first few lanthanides.

That gives rise to the following rationales:

• `"La"` and `"Ce"` have an electron in their `5d` instead of `4f` because the `4f` is more radially compact, and given the small difference in energy between them (about `"6.8 eV"`), it is more energetically favorable to choose the `5d`, which is radially more diffuse.

• `"Gd"` has about a `"16 eV"` `4f-5d` energy gap, and apparently, the electron repulsion it would generate to add another `4f` electron, combined with the radial compactness of the `4f` orbitals, is enough that it would rather have that electron in the `5d`.