What is the electron configuration for the f block?
2 Answers
The f block has the lower level filled, then for valance electrons has 2 s electrons 1 d electron and then up to 14 f electrons filling the 7 f orbitals.
I finally feel confident enough to post a table of the configurations, along with some detailed rationale for why the configurations are so riddled with 'Aufbau exceptions'.
For reference, the energy scales I will be using are small. For perspective, you can compare the numbers with the first ionization energy of
The following graphs are from page
DISCLAIMER: LONG ANSWER!
LANTHANIDES
The order by atomic number is down the first column, and then down the second column. In
#color(white)([(color(red)(La),(color(red)([Xe] 6s^2 5d^1)),color(black)(Tb),(color(black)([Xe] 6s^2 4f^9))),(color(red)(Ce),(color(red)([Xe] 6s^2 4f^1 5d^1)),color(black)(Dy),(color(black)([Xe] 6s^2 4f^10))),(color(black)(Pr),(color(black)([Xe] 6s^2 4f^3)),color(black)(Ho),(color(black)([Xe] 6s^2 4f^11))),(color(black)(Nd),(color(black)([Xe] 6s^2 4f^4)),color(black)(Er),(color(black)([Xe] 6s^2 4f^12))),(color(black)(Pm),(color(black)([Xe] 6s^2 4f^5)),color(black)(Tm),(color(black)([Xe] 6s^2 4f^13))),(color(black)(Sm),(color(black)([Xe] 6s^2 4f^6)),color(black)(Yb),(color(black)([Xe] 6s^2 4f^14))),(color(black)(Eu),(color(black)([Xe] 6s^2 4f^7)),color(black)(Lu),(color(black)([Xe] 6s^2 4f^14 5d^1))),(color(red)(Gd),(color(red)([Xe] 6s^2 4f^7 5d^1)),"","")])#
The exceptions can be explained by looking at how the energies of the
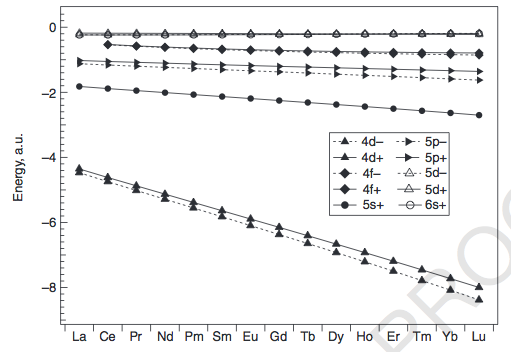
We can see that the
The radii of the
The exceptions occur mainly for the earlier lanthanides (
-
The radial compactness of the
#4f# orbitals makes it more favorable to fill the#6s# and#5d# first for#La# and#Ce# , to minimize electron repulsion. -
For
#Gd# , the repulsion that would be generated from pairing a#4f# electron would be enough to promote it to a#5d# orbital (about#0.6# #E_h# away, or about#"16 eV"# ), so#Gd# takes on a#f^7 d^1# configuration instead of#f^8 d^0# .
ACTINIDES
The order by atomic number is down the first column, and then down the second column. In
#color(white)([(color(red)(Ac),(color(red)([Rn] 7s^2 6d^1)),color(black)(Bk),(color(black)([Rn] 7s^2 5f^9))),(color(red)(Th),(color(red)([Rn] 7s^2 6d^2)),color(black)(Cf),(color(black)([Rn] 7s^2 5f^10))),(color(red)(Pa),(color(red)([Rn] 7s^2 5f^2 6d^1)),color(black)(Es),(color(black)([Rn] 7s^2 5f^11))),(color(red)(U),(color(red)([Rn] 7s^2 5f^3 6d^1)),color(black)(Fm),(color(black)([Rn] 7s^2 5f^12))),(color(red)(Np),(color(red)([Rn] 7s^2 5f^4 6d^1)),color(black)(Md),(color(black)([Rn] 7s^2 5f^13))),(color(black)(Pu),(color(black)([Rn] 7s^2 5f^6)),color(black)(No),(color(black)([Rn] 7s^2 5f^14))),(color(black)(Am),(color(black)([Rn] 7s^2 5f^7)),color(black)(Lr),(color(black)([Rn] 7s^2 5f^14 6d^1))),(color(red)(Cm),(color(red)([Rn] 7s^2 5f^7 6d^1)),"","")])#
We can again examine the energies (pg. 199):
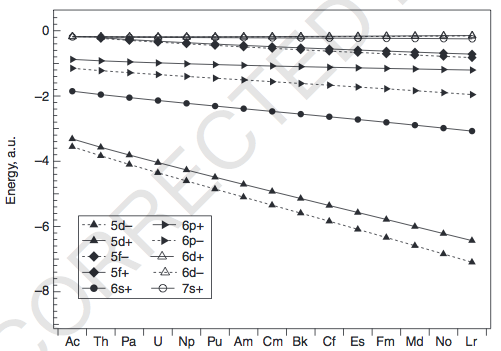
The energies of the
That makes the energetic degeneracies of the
As before, the exceptions occur mainly for the earlier actinides (
- For
#Ac-Th# , since the#5f# 's and#6d# 's are very similar in energy, it is possible for#6d# occupation instead of the#5f# . I believe it is because the#5f# orbitals are barely bigger than the#6p# ,#6s# , and#5d# orbitals for#Th# that the#5f# is about as core-like as them and thus not as accessible to fill... but this is difficult to explain.
You can see the radial extents here (pg. 202):
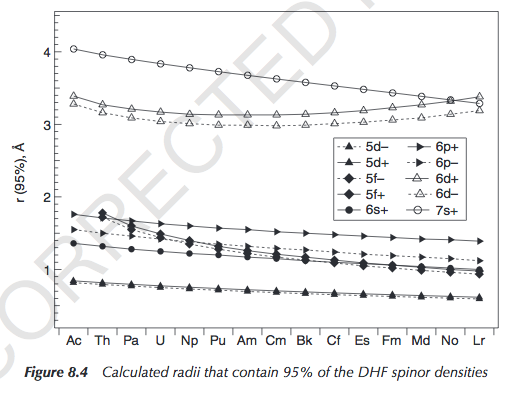
"Spinor" just means an electronic quantum state (in the Pauli Exclusion sense) with a specific spin (up/down). DHF stands for Dirac-Hartree-Fock.
-
For
#Pa - Np# , whose#6d-5f# gap is even smaller than the#5d-4f# gap of the lanthanides (but bigger than for#Ac-Th# ), I believe that the repulsions generated from adding a second electron into the#6d# orbitals (even without pairing) are still enough that since the#5f# orbitals are lower in energy, it is preferable to proceed by filling them instead. -
And again for
#Cm# , similar to#Gd# , the electron repulsion that occurs with pairing an#5f# electron would be enough to promote it to a#6d# orbital (about#0.15# #E_h# away, or about#"4 eV"# ).

