What is the osmotic pressure for #"1.95 g"# of sucrose dissolved in #"150 mL"# solution at #25^@ "C"#? #"FW"# #=# #"342.2965 g/mol"#

1 Answer
Truong-Son N.
May 31, 2017

#Pi = "0.9292 atm"#.

You can read more about osmotic pressure (and other colligative properties) here.

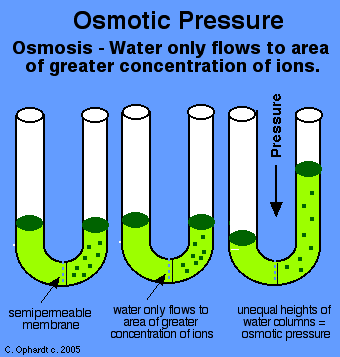
The osmotic pressure #Pi#, the pressure needed to stop the solvent flow from low to high concentration across a semi-permeable membrane, is given by:

#Pi = icRT#,

where:

  • #i# is the van't Hoff factor, as seen in freezing point depression and boiling point elevation. It can be approximated by the number of particles per formula unit in solution.
  • #c# is the concentration in whatever units are appropriate. In this case, if #Pi# is in #"atm"#, then #c# is in #"mol/L"# when...
  • ...the universal gas constant #R# is #"0.082057 L"cdot"atm/mol"cdot"K"#.
  • #T# is the temperature in #"K"#.

http://1.bp.blogspot.com/

We are indeed given the correct info to calculate the molarity of the sucrose solution.

#1.95 cancel"g suc" xx "1 mol suc"/(342.2965 cancel"g suc")#

#=# #"0.005697 mols suc"#

So, the molarity is:

#c = "0.005697 mols suc"/(150 xx 10^(-3) "L soln")#

#=# #"0.03798 M"#

Therefore, the osmotic pressure at #25^@ "C" = "298.15 K"# for the NONELECTROLYTE sucrose is:

#color(blue)(Pi) = (1)(0.03798 cancel"mol/L")(0.082057 cancel"L"cdot"atm/"cancel"mol"cdotcancel"K")(298.15 cancel"K")#

#=# #color(blue)("0.9292 atm")#,

since nonelectrolytes have #i = 1#, having hardly any further dissociation at all.

Related questions
See all questions in Osmolarity
Impact of this question
13291 views around the world
You can reuse this answer
Creative Commons License