What happens as reactants get consumed while approaching a chemical equilibrium?
1 Answer
The rate of reaction decreases over time as the reactants get consumed. Eventually the forward rate equals the backwards rate.
In kinetics, we consistently use the initial rate of reaction for this very reason; the rate of reaction decreases as the reactants get consumed in the reaction since they have a harder time of finding each other to collide successfully.
#underbrace(overbrace(r(t))^"initial rate" = overbrace(k)^"rate constant " cdot overbrace([A]^m[B]^n)^"reactants and their orders")_("rate law")#
(Recall that successful collisions of a high fraction of molecules with a high enough energy results in a chemical reaction.)
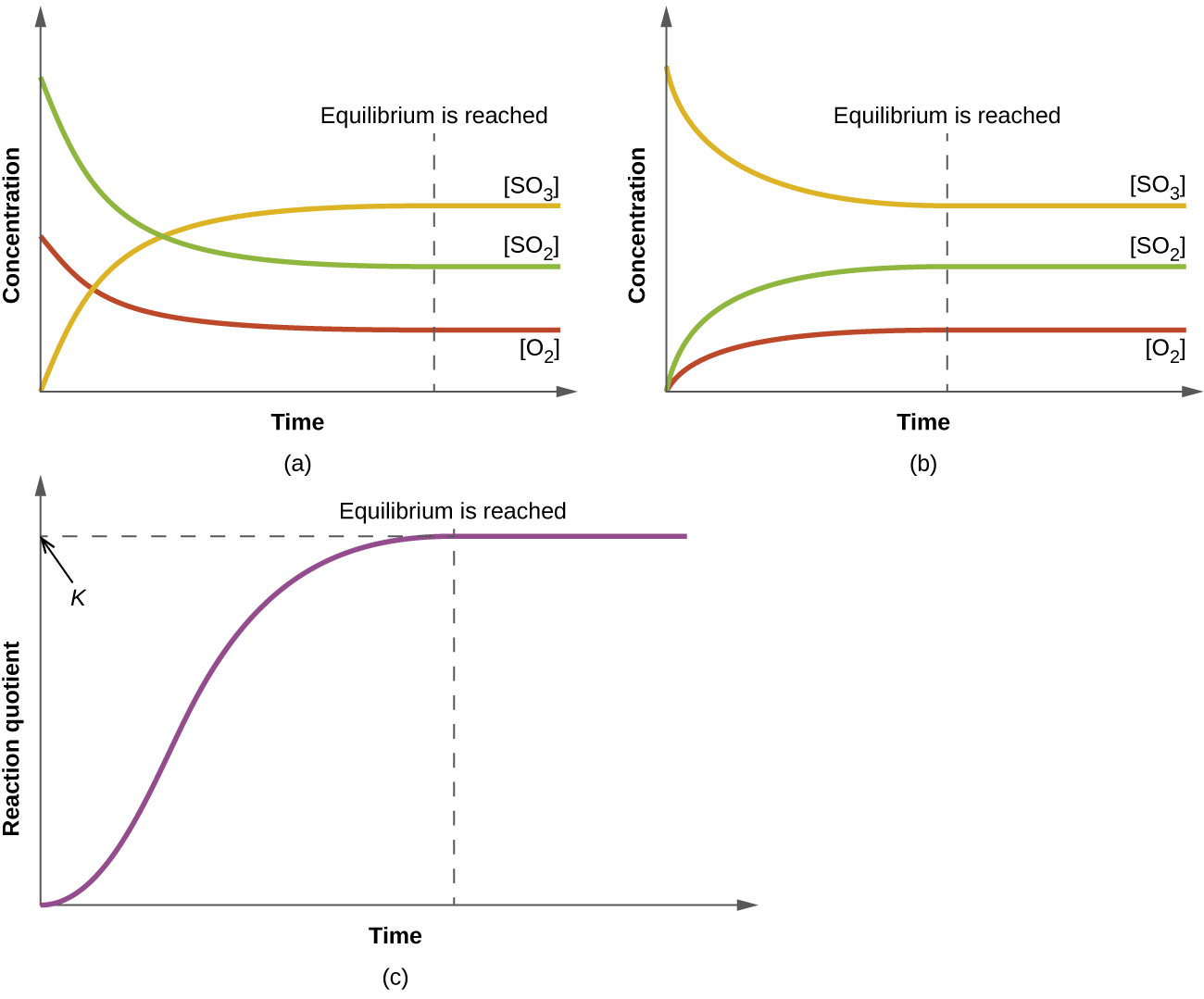
Here we have three graphs that are basically showing the same thing: reactions reach equilibrium if you give them enough time, and that is because the forward rate becomes equal to the backwards rate of reaction.
This is shown in the convergence of the changes in concentration to become flat lines.
#(a)# shows some amount of#"O"_2# and#"SO"_2# reaching equilibrium with the generated#"SO"_3# (that started at zero concentration). The reaction shown is:
#2"SO"_2(g) + "O"_2(g) rightleftharpoons 2"SO"_3(g)#
#(b)# shows the same reaction in reverse, and we start with all#"SO"_3# instead:
#2"SO"_3(g) rightleftharpoons 2"SO"_2(g) + "O"_2(g)#
#(c)# shows the progression of the reaction quotient#Q# towards equalling#K# , and when that is the case, the reaction is at equilibrium (when#Q = K# ).

