Question #91ae7
1 Answer
Well, the Bohr model ONLY works for the hydrogen atom, so this is only useful for the hydrogen atom... or atoms with one electron (which are not that useful).
For multi-electron atoms, we must account for electron correlation, which splits the orbitals by their angular momentum (e.g.
Clearly, a given
We know the Rydberg equation
#DeltaE = E_(n_f) - E_(n_i) = -"13.6 eV"(1/n_f^2 - 1/n_i^2)# ,
which is really just using initial and final states
So, taking only one of these states gives
#bb(E_n = -(13.6 "eV")/(n^2))#
for the energy level for the principal quantum number
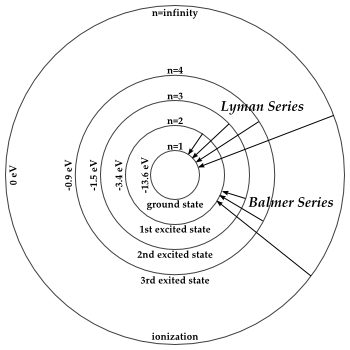
You can see this work for the hydrogen atom.
#E_2 = -"13.6 eV"/(2^2) = -"3.4 eV"#
#E_3 = -"13.6 eV"/(3^2) = -"1.51 eV" ~~ -"1.5 eV"#
#E_4 = -"13.6 eV"/(4^2) = -"0.85 eV" ~~ -"0.9 eV"#
etc.

