At what absolute temperatures do molecules occupy each energy level?

1 Answer
Truong-Son N.
Jul 19, 2017

At absolute what temperature? Absolute temperature is in units of #"K"#, kelvins. It depends on what temperature you are at that certain molecules have access to certain kinds of energy levels, and thus can have that kind of energy.

  • All molecules have translational energy at most temperatures, except #"0 K"#.
  • All molecules have ONLY vibrational energy at #"0 K"#.
  • As you increase the temperature from #"0 K"#, molecules begin to gain rotational energy (usually before #"100 K"#), and at really high temperatures (a few thousand #"K"#), they gain vibrational energy.
  • At really, really, really high temperatures (tens of thousands of #"K"#, probably), they gain electronic energy.

DISCLAIMER: LONG ANSWER!

The most common different kinds of energies are:

  • translational
  • rotational
  • vibrational
  • electronic

These energy levels are in general differently spaced as follows:

#"electronic"# #">>"# #"vibrational"# #># #"rotational"# #">>"# #"translational"#

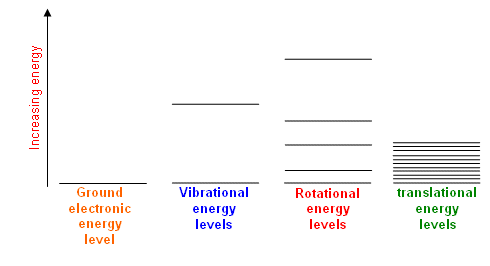
http://www.4college.co.uk/

For the temperatures that we care about, these temperatures are called the rotational and vibrational temperatures, #Theta_(rot)# and #Theta_(vib)#, but I suppose we can define an "electronic temperature" #Theta_(el ec)#.

We have:

#Theta_(rot) = (B_e)/(k_B)# in units of #"K"#, usually in the tens of #"K"#

#Theta_(vib) = (omega_e)/(k_B)# in units of #"K"#, usually in the hundreds or thousands of #"K"#

#Theta_(el ec) = (T_e)/(k_B)# in units of #"K"#, usually in the upper thousands or tens of thousands of #"K"#

where:

  • #B_e# is the rotational constant in #"cm"^(-1)# for each type of rotational motion (up to #2# for linear molecules and #3# for nonlinear molecules).
  • #omega_e# is the fundamental vibrational frequency in #"cm"^(-1)# for each vibration (the number of vibrational motions are #3N - 5# for linear polyatomic molecules and #3N - 6# for nonlinear polyatomic molecules, where #N# is the number of atoms).
  • #T_e# is the electronic frequency constant (or whatever it's called), and is analogous.
  • #k_B ~~ "0.695 cm"^(-1)"/K"# is the Boltzmann constant in #"cm"^(-1)"/K"#.

And when these temperatures are surpassed, the molecule has that kind of energy.

In summary...

  • All molecules have translational energy at most temperatures, except #"0 K"#.
  • All molecules have nonzero vibrational energy at #"0 K"#.
  • As you increase the temperature from #"0 K"#, molecules begin to gain rotational energy (usually before #"100 K"#), and at really high temperatures (a few thousand #"K"#), they gain vibrational energy.
  • At really, really, really high temperatures (tens of thousands of #"K"#, probably), they gain electronic energy.

EXAMPLE MOLECULE: CO

As an example (http://webbook.nist.gov/cgi/cbook.cgi?ID=C630080&Units=SI&Mask=1000):

  • #"CO"# has a rotational frequency at around #"1.93 cm"^(-1)#, so only past around

#"1.93 cm"^(-1)/("0.695 cm"^(-1)"/K") ~~ ul"2.78 K"#

would it rotate from natural surrounding heat.

  • #"CO"# has a vibrational frequency at around #"2169.8 cm"^(-1)#, so only past around

#"2169.8 cm"^(-1)/("0.695 cm"^(-1)"/K") ~~ ul"3122 K"#

would it vibrate from natural surrounding heat.

  • #"CO"# has its first excited-state electronic energy level about #"48686.7 cm"^(-1)# above the ground state, which means it won't be until at least

#"48686.7 cm"^(-1)/("0.695 cm"^(-1)"/K") ~~ ul"70000 K"#

or so before #"CO"# has electronic energy naturally from surrounding heat.

Related questions
See all questions in Temperature Scales
Impact of this question
4609 views around the world
You can reuse this answer
Creative Commons License