Question

Question #65c61

Answer 1

Ok I tried also the last part although I am not 100% sure.
(Check my maths anyway).

Explanation:

Ok,
The work function is the energy you need to supply to a metal to at least free its electrons (not move away). Basically, consider a metal as a sponge (the lattice) full of molecules of water (the free electrons) you can shine light on a metal and in doing so give energy (light carries energy) to the free electrons. They will be bound to the metal BUT if you give enough energy (work function) you'll be able to free the electros (at least on the surface).

Now, consider that light carries energy of the form:
`E=hf`
where:
`h=6.63xx10^-34Js` is Planck's Constant;
`f=` frequency.
In question b1 we use the relationship between frequency `f`, wavelength `lambda` and speed of light in vacuum `c=3xx10^8m/s` as:
`c=lambdaf`
to find the energies:
as
`E=hc/lambda`

So, for example, for red `lambda=760nm=760xx10^-9m` we get:
`E_("red")=6.63xx10^-34*(3xx10^8)/(760xx10^-9)=2.6xx10^-19J`

{try by yoursef for the other two]

Question c) it's easier than it looks:
evaluate the energies for violet and yellow (red we already found) but in eV (in your table is in eV) and see which one wins. In case of red the energy in eV is:
`E_("red")=(2.6xx10^-19)/(1.6xx10^-19)=1.62eV`
so we see that this energy is not enough to free electrons (it is smaller than any work function).
Try with the othe colours.

Hi I am back!
I tried with some maths but I am quite rusty so take it as a hint more than a definite answer.
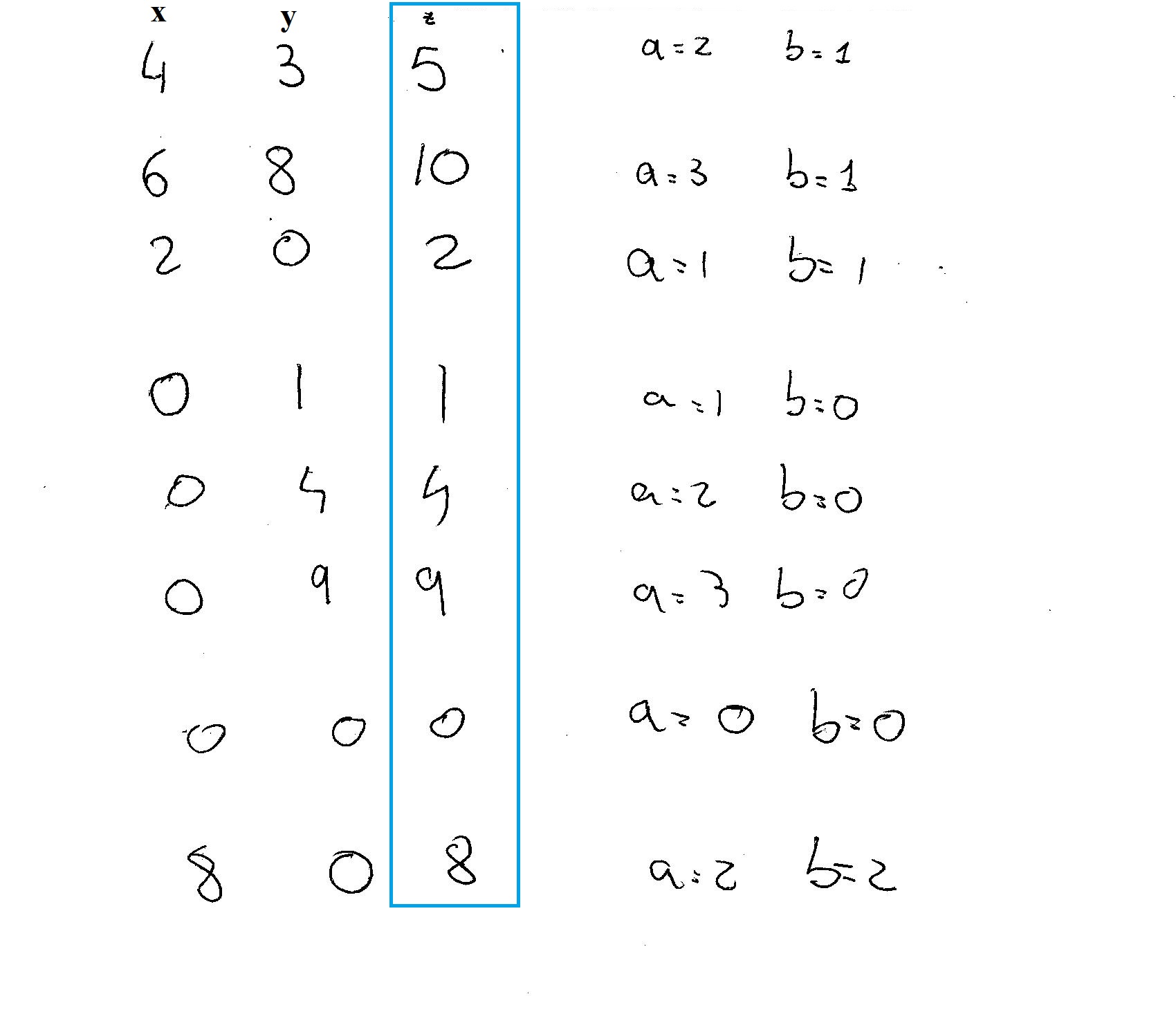
Ok I discovered that the three integers are relates through two values `a and b` so that you can build all the integer triplets `x,y andz`.
The triplets can be build as:
`x=2ab`
`y=a^2-b^2`
`z=a^2+b^2`
so what I did was to give values to `a and b` to evaluate the `x, y, and z` with the restrain that `z^2<=100` so that `z` cannot be bigger than `10`
I got 8 possibilities: