What is the difference between localized and delocalized electron density?
1 Answer
Well, consider delocalization of electron density. That is when electron density is spread as much as possible throughout a molecule, so that the minimum charge buildup is present in a given orbital.
That is described:
- collectively by all the resonance contributors in Lewis structures.
- collectively by all the individual molecular orbital contributions in molecular orbital diagrams.
(There are subtle differences between these, but these are roughly analogous for simplicity. See here for more detail.)
Electron density localization is the lack of that.
It is when we stuff all the electron density into a few orbitals, instead of spreading it out, and it almost never really happens in a real molecule or quantum system (even if there is no resonance going on).
EXAMPLE WITH RESONANCE STRUCTURES
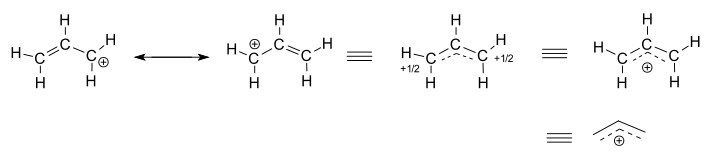
Consider the isolated (not-reacting) allyl cation,
 https://upload.wikimedia.org/
https://upload.wikimedia.org/
- The left two structures are resonance contributors, each of which are localized representations of the true delocalized structure.
- The three right-hand structures are each representations of the resonance hybrid structure, or the delocalized structure.
The delocalized structure is basically described by a collection of bonding molecular orbitals.
EXAMPLE WITH A MOLECULAR ORBITAL DIAGRAM
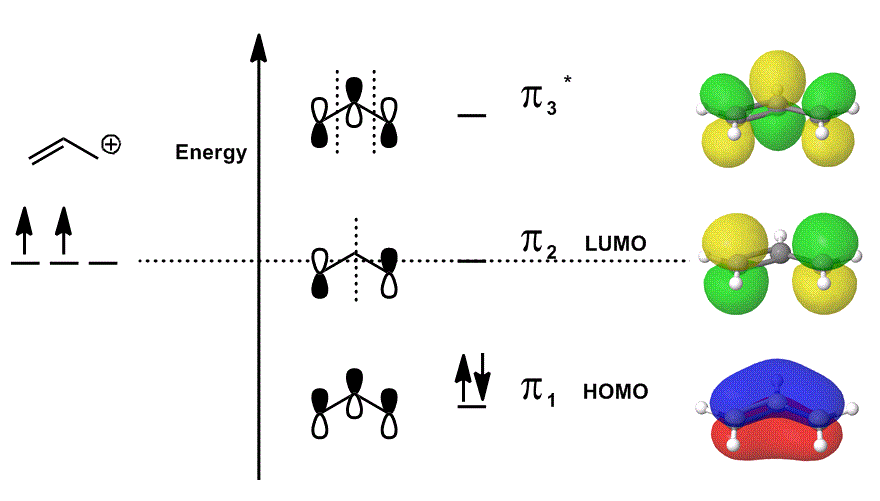
Consider the allyl cation again in an MO diagram that ONLY describes the
 https://chemistry.stackexchange.com/
https://chemistry.stackexchange.com/
- Each of the orbital contributions in the middle are depicted localized; the atomic orbitals that would overlap are shown as themselves (phase included).
- Each of the orbitals on the far right (one per row) are depicted delocalized; the electron density is allowed to spread out so that the molecular orbitals are depicted with complete consideration of overlaps, nodes and phases.
When you overlap
Psi_("allyl"^(+)) = c_1overbrace(pi_1)^"bonding" + c_2overbrace(pi_2)^"nonbonding" + c_3overbrace(pi_3^"*")^"antibonding" and
Psi_("allyl"^(+)) then describes the overall distribution of states that collectively describe the reactivity of the allyl cation.
In other words,

