Question #9ff5f
1 Answer
Explanation:
Right from the start, you know that your solution interval cannot include
So you know that you need to have
Now, let's separate this compound inequality into two inequalities
#-1 < (x+1)/(x-1) " " and " " (x + 1)/(x-1) < 0#
Remember, the solution interval must satisfy both inequalities!
For the first inequality, you know that
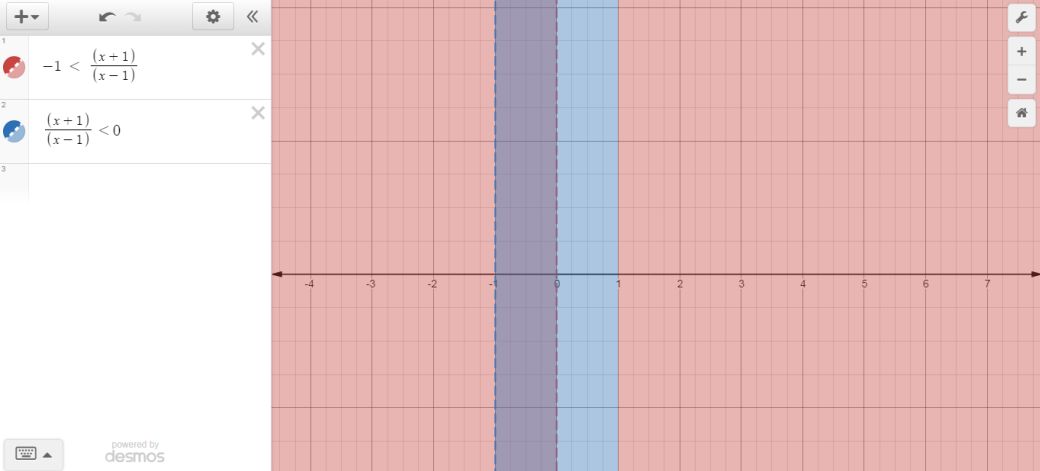
#-1 < (x+1)/(x-1)#
Now, it is absolutely vital to keep in mind that we can have
#ul(x -1 < 0)# In this case, the first inequality can be rewritten as
#-1 * (x-1) color(red)(>) x+1# Notice the fact that we must flip the sign of the inequality because we're multiplying on both sides by a negative number, since
#x - 1 < 0# .This simplifies to
#-x + 1 > x + 1#
#-2x > 0 implies x < 0" "color(blue)((1))#
#ul(x - 1 >0)# In this case, the first inequality can be written as
#-1 * (x-1) < (x+1)# This simplifies to
#-x + 1 < x + 1#
#-2x < 0 implies x > 0# However, keep in mind that in this case, we need
#x - 1 > 0 implies x > 1# so you can say that
#x > 1" "color(blue)((2))# So in order for the first inequality to be true, you need
# overbrace((-oo", " 0))^(color(blue)("from (1)")) " " or " " overbrace((1", " oo))^(color(blue)("from (2)"))" "color(darkorange)("( * )")#
For the second inequality, you know that
#(x+1)/(x-1) < 0#
The same approach applies here as well--you have two possible cases to look at.
#ul(x-1 < 0)# In this case, you have
#x + 1 color(red)(>) 0 * (x-1)# This simplifies to
#x + 1 > 0 implies x > -1# Since you also need
# x - 1 < 0 implies x < 1# you can say that you have
# -1 < x < 1" "color(darkgreen)((1))#
#ul(x - 1 > 0)# In this case, the second inequality can be rewritten as
#x+ 1 < 0 * (x-1)# This simplifies to
#x + 1 < 0 implies x < -1# But since you also need
#x - 1 > 0 implies x > 1# you can say that you have
#1 < x < -1 implies x in {O/}" "color(darkgreen)((2))# According to
#color(darkgreen)((1))# and#color(darkgreen)((2))# , the second inequality is only satisfied by
#x in (-1, 1)" "color(darkorange)("(* *)")#
Finally, to find the solution interval for the compound inequality, you need to intersect the
You have
#(- oo, 0) " " or " " (1, oo)" " and " " (-1, 1)#
the equivalent of
#(- oo, 0) " " uu " " (1, oo)" " nn " " (-1, 1)#
which gets you
#x in (-1, 0)#
To double-check the result, you can either graph the two inequalities separately and intersect their solution intervals, or graph the compound inequality and look at the solution interval.
The graph for
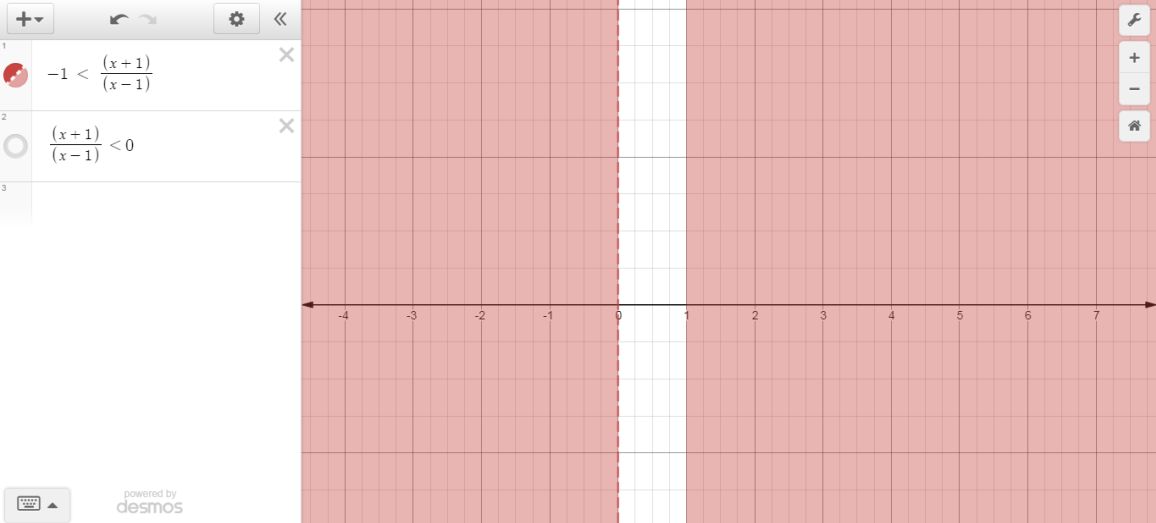
The graph for
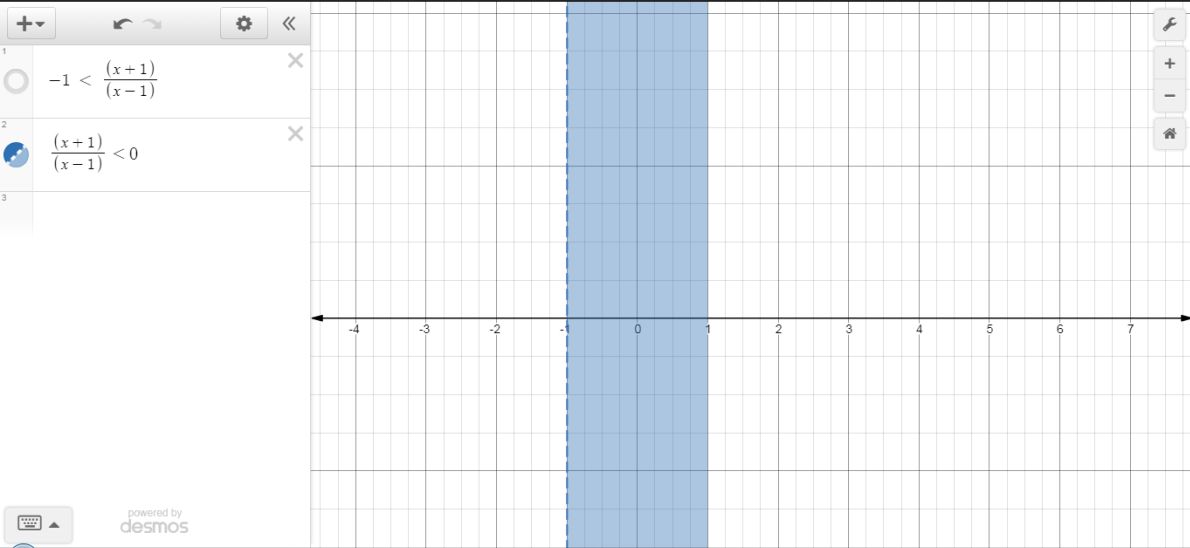
and the graph for the compound inequality looks like this