Question #c7d56

1 Answer
Sridhar V.
Dec 9, 2017

#color(red)(y = -5x+15)#

Please refer to the data set chosen, an example, to understand the mathematical process involved in finding the Slope and the intercept of a linear relationship.

Explanation:

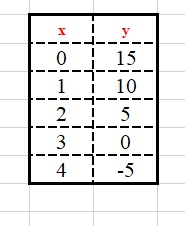
We will consider the following data set for our solution:

Table.1
enter image source here

Note: When you graph a linear relationship, the graph is a straight line.

Slope (or) Gradient represents the rate of change of our straight line.

Hence, Slope is represented by a Change in y over a Change in x:

Slope = Change in y#/# Change in x (or)

Slope = #(rise)/(run)# (or)

Slope = #(Delta y)/(Delta x)#

y-intercept is where the graph is going to cross the y-axis.

The Slope-Intercept Equation is given by the formula

#color(blue)(y = mx + b)# #color(red)(..Equation.1)#

where #color(blue)(m)# is our Slope and #color(blue)(b)# is our y-intercept

#color(green)(Step.1)#

in this step, we will now investigate for the Change in y in our table of values available in Table 1

What happens when we move from the first value of #y# to the second value of #y#?

Table.2
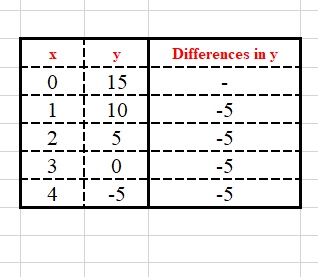
enter image source here

We can see that the differences are #color(blue)(-5)# among the y-values.

Hence #(Delta y) = -5# #color(red)(..Equation.2)#

#color(green)(Step.2)#

In this step, we will find out whether there is a Constant Rate of Change for our x-values

Table.3

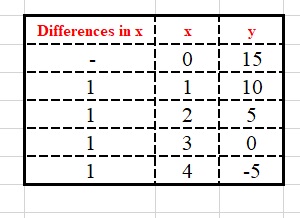
enter image source here

Observe that we do have a constant rate of change for our x-values.

Hence #(Delta x) = 1# #color(red)(..Equation.3)#

#color(green)(Step.3)#

In this step, we are ready to find our Slope

Using our equations #color(red)(Equation.2 and Equation.3)# we can write

Slope = #(Delta y)/(Delta x)#

Slope #= -5/1 = -5#

Hence, our Slope(m) = -5... Result.1

#color(green)(Step.4)#

Our y-intercept is when our graph (in our example, it is a straight line) is crossing the y-axis

We know that when our graph crosses the y-axis our #x# value will be zero(0)

From our Table.1 , we understand that #x = 0# when the corresponding #y.value = 15#

Hence, our y-intercept = 15 ... Result.2

It means that this is the point on our y-axis where our graph will cross through.

#color(green)(Step.5)#

In this step, we are ready to write the Equation of our linear relationship, in the slope-Intercept Form

Using #color(red)(..Equation.1)# and our intermediate results, Result.1 and Result.2 we obtain

#color(blue)(y = mx + b)#

#color(red)(y = -5x+15)# our final answer.

Related questions
Impact of this question
889 views around the world
You can reuse this answer
Creative Commons License