Question

What is the energy of gases at `"0 K"`?

Answer 1

Well, ignoring relativity, the total energy of a molecular gas would never be zero at `"0 K"`, but the total energy of an atomic gas could be close to zero in deep space.

Being exact, even an atomic gas could interact with another one to generate a small gravitational potential energy, making the total energy still nonzero.

---

The total nonrelativistic energy `E` involves the potential energy `K`, kinetic energy `V`, and internal energy `U`, i.e.

`E = K + V + U`,

where `K` and `V` are macroscopic (not molecular), and `U` is internal to the system.

EXTERNAL KINETIC ENERGY

The external kinetic energy is primarily influenced by the transfer of internal translational kinetic energy amongst particles, which is discussed below.

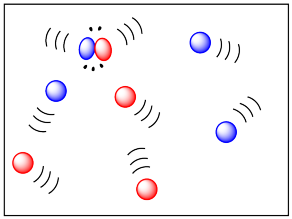
For atoms, this is zero, but for molecules, this is not quite zero due to the internal vibrational energy (which is also mentioned below).

[Note that it is also possible that at `"0 K"`, even though the average kinetic energy might be zero, it is not necessarily true that all the individual external kinetic energies are zero (there may be fortuitous cancellation).]

EXTERNAL POTENTIAL ENERGY

If the system is completely isolated from any external fields (gravitational, electric, magnetic, etc) and other systems, then the macroscopic potential energy is zero, so maybe in deep space, `V ~~ 0`.

But then again, two mass-ive bodies can create a small gravitational force:

`F_G = (Gm_1m_2)/r_(12)`, `" "G = 6.67 xx 10^(-11) "m"^3 cdot "kg"^(-1) cdot "s"^(-2)`

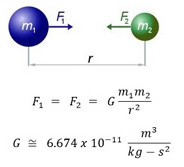
So the system would have to contain only one particle, to not generate this interaction force with anything else.

That is really not ordinarily possible... everything nanoscopic particle is surrounded by at least one other thing, even in deep space.

INTERNAL ENERGY OF THE SYSTEM

The internal energy would include all components: translational, rotational, vibrational, electronic, and nuclear degrees of freedom.

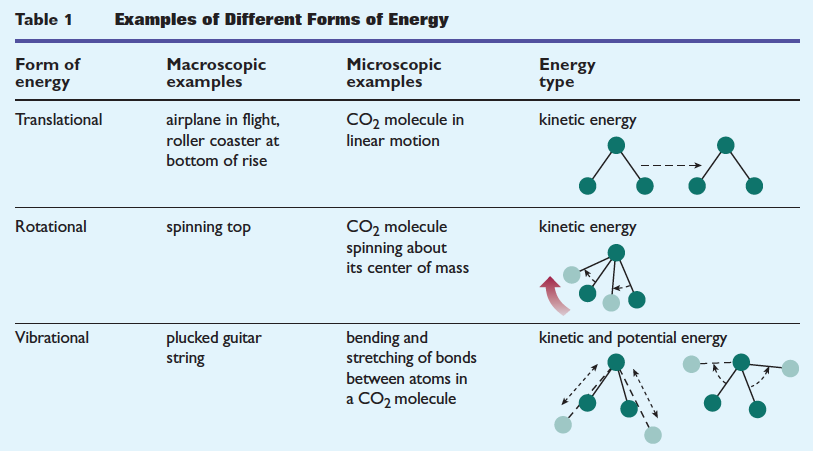
As for electronic internal energy, it is often inaccessible, but sometimes low-lying states are available (such as for diatomic iodine).

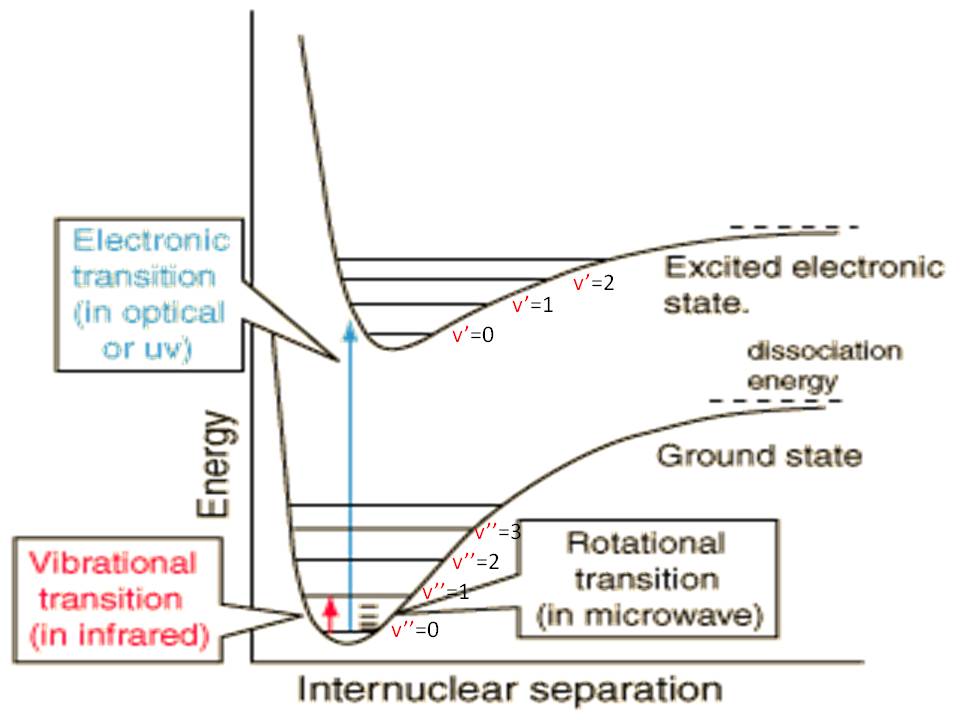
The above image lets you know the relative sizes of the energy scales (rotational, vibrational, electronic). Translational energy level spacings are typically much denser than rotational energy level spacings.

In general,

• For an atom at `"0 K"`, all of these are zero.
• For a diatomic molecule at `"0 K"`, the vibrational zero-point energy is `1/2hnu`. For example, one molecule of `"HCl"` at `"0 K"` has a vibrational zero-point energy of `2.97 xx 10^(-20) "J"`.

So for atoms, this can be zero at `"0 K"`. For molecules, absolutely not.