Question #f307f
1 Answer
Explanation:
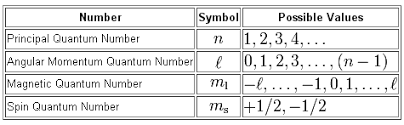
The first quantum number set given to you is not correct because the spin quantum number,
#m_s = {+1/2, - 1/2}#
So the quantum number set that has
#m_s = +1#
cannot be used to describe the location and the spin of an electron inside an atom.
The second quantum number set is also incorrect because the angular momentum quantum number,
Similarly, the third quantum number set is incorrect because the angular momentum quantum number cannot take a negative value.
More specifically, the angular momentum quantum number can take
#l = {0, 1, ..., n-1}#
So the quantum number set that has
#n=1, l =1#
is not valid because the value of the angular momentum quantum number is not possible given the value of the principal quantum number.
The set that has
#l = -3#
is not valid because of the negative value assigned to the angular momentum quantum number.
The fourth quantum number set is correct because all the four quantum numbers take accepted values.
#n = 3, l = 2, m_l = 1, m_s = -1/2# This set describes an electron located in the third energy shell, in the
#3d# subshell, let's say in the#3d_(xy)# orbital, that has spin-down.
The value of the magnetic quantum number,
#m_l = {-l, -(l-1),..., -1, 0, 1, ..., (l-1), l}#
So for
#l = 2#
you can have
#m_l= 1#
as a valid value for the magnetic quantum number.

