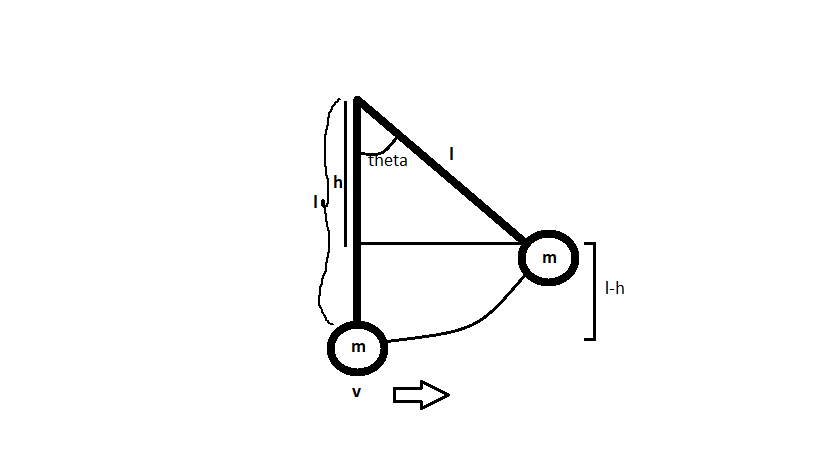
See the diagram made,where a pendulum of string length l and a bob of mass m reaches up to the shown position from its mean point,and at the mean position, it had a velocity of v
So,vertically it has shifted a distance of (l-h) (from the diagram)
Now, h/l = cos theta or, h = l cos theta ,so (l-h) = l(1-cos theta)
Now, in its pathway,energy will be conserved.
So,at its mean position,total energy is kinetic energy i.e 1/2mv^2
And, at the highest point,its total energy is purely potential energy i.e mg(l-h) i.e mgl(1-cos theta)
So,equating both we get,
v=sqrt(2gl(1-cos theta)
ALTERNATIVELY,
Suppose, a particle in S.H.M follows the equation,
x= a sin omegat ......1 (here,a is the amplitude of its motion)
For,a simple pendulum, omega = sqrt(g/l),where g is acceleration due to gravity and l is the length of the pendulum)
So, its velocity equation will be, v=aomega cos omegat (by differentiating 1, as v=(dx)/dt
From 1 we can say cos omegat = sqrt(1-(x/a)^2) (as sin^2omegat+cos^2omegat=1)
So,putting the value of cosomegat in the velocity equation,we get,
v=omegasqrt(a^2-x^2) ....2
Now, for the given equation, x=asinomegat, mean position is at x=0
So,putting x=0 in equation 2 we get, v=omegaa
This the equation of the velocity of a particle under SHM at its mean position.
Now, see maximum value of v in the equation 2 will come,when x will be zero,so maximum value of v becomes omegaa
That means,velocity is the maximum in the mean position as well.


