What is #int \ (sinx+cosx)/sqrt(1+sin2x) \ dx #?
2 Answers
Explanation:
=
=
=
=
# int \ (sinx+cosx)/sqrt(1+sin2x) \ dx = arctan tanx + C #
Explanation:
In addition to the existing solution:
We seek:
# I = int \ (sinx+cosx)/sqrt(1+sin2x) \ dx #
Using the trigonometric Identity:
# sin^2A+ cos^2A -= 1#
We can manipulate the integral as follows:
# I = int \ (sinx+cosx)/sqrt(1+2sinxcosx) \ dx #
# \ \ = int \ (sinx+cosx)/sqrt(sin^2x+ cos^2x+2sinxcosx) \ dx #
# \ \ = int \ (sinx+cosx)/(sqrt((sinx+cosx)^2)) \ dx # ..... [A]
We may be tempted to continue as follows:
# I = int \ (sinx+cosx)/(sqrt((sinx+cosx)^2)) \ dx #
# \ \ = int \ (sinx+cosx)/(sinx+cosx) \ dx #
# \ \ = int \ 1 \ dx #
# \ \ = x+c # ..... [B]
However, There now two issues that require further analysis:
(1) There are discontinuities in the integrand when:
# sinx+cosx = 0 => tanx=-1 => x=npi-pi/4 #
e.g at#x=(-5pi)/4, -pi/4, (3pi)/4, (7pi)/4 # (2) Any linear combination of periodic functions is itself periodic, further, any linear combination of sinusoidal functions is also sinusoidal. The introduction of the square in the denominator causes it be positive
#AA x in RR# , thus:if
#{ (sinx+cosx<0, =>, "Integrand " < 0), (sinx+cosx=0, =>, "Integrand is undefined"), (sinx+cosx>0, =>, "Integrand " > 0) :} #
We can graph the function as follows, and we discover it represents a "saw tooth" with period
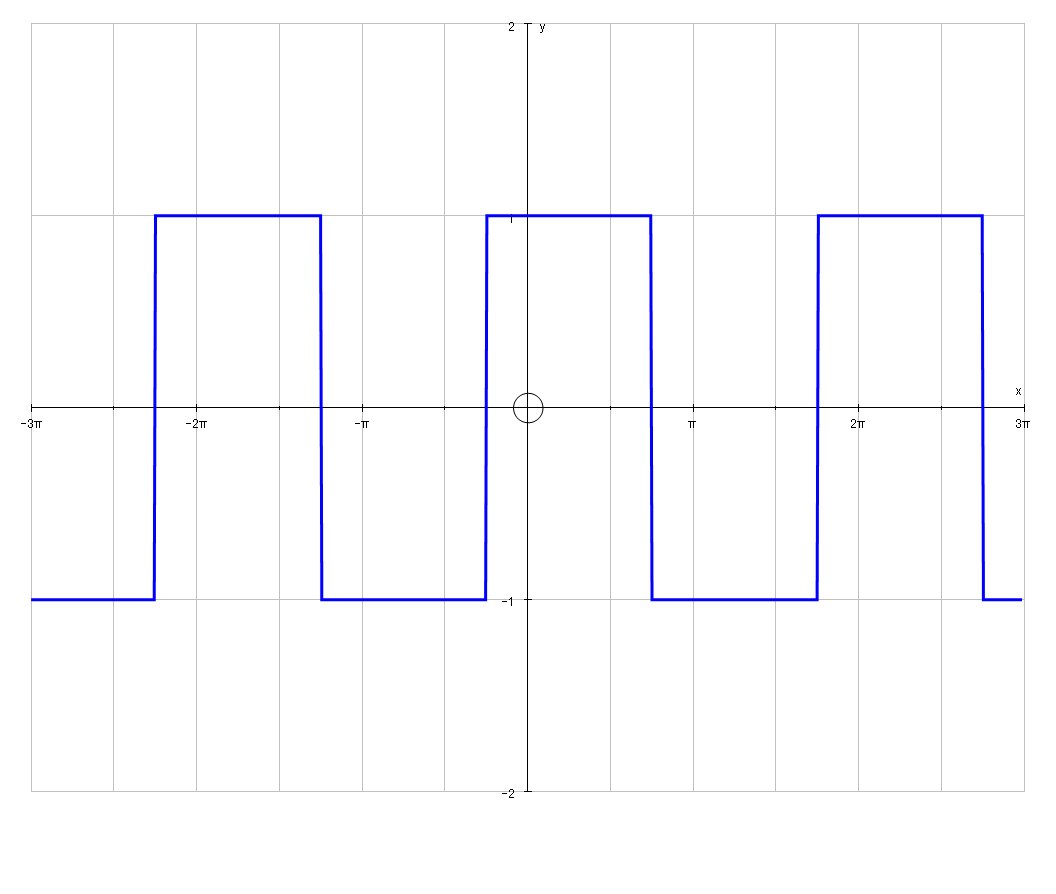
Consequently, we expect the solution to the integral to be periodic, and this is not reflected in the naive solution [B]
Instead, we evaluate the integral as follows:
# I = int \ (sinx+cosx)/sqrt(1+2sinxcosx) \ dx #
Perform a substitution
# I = int \ 1/(1+u^2) \ du #
# \ \ = arctan u + C #
# \ \ = arctan tanx + C #
# \ \ != x + C \ \ AA x in RR#
And we can graph the the integral result (in red) alongside the original periodic function:
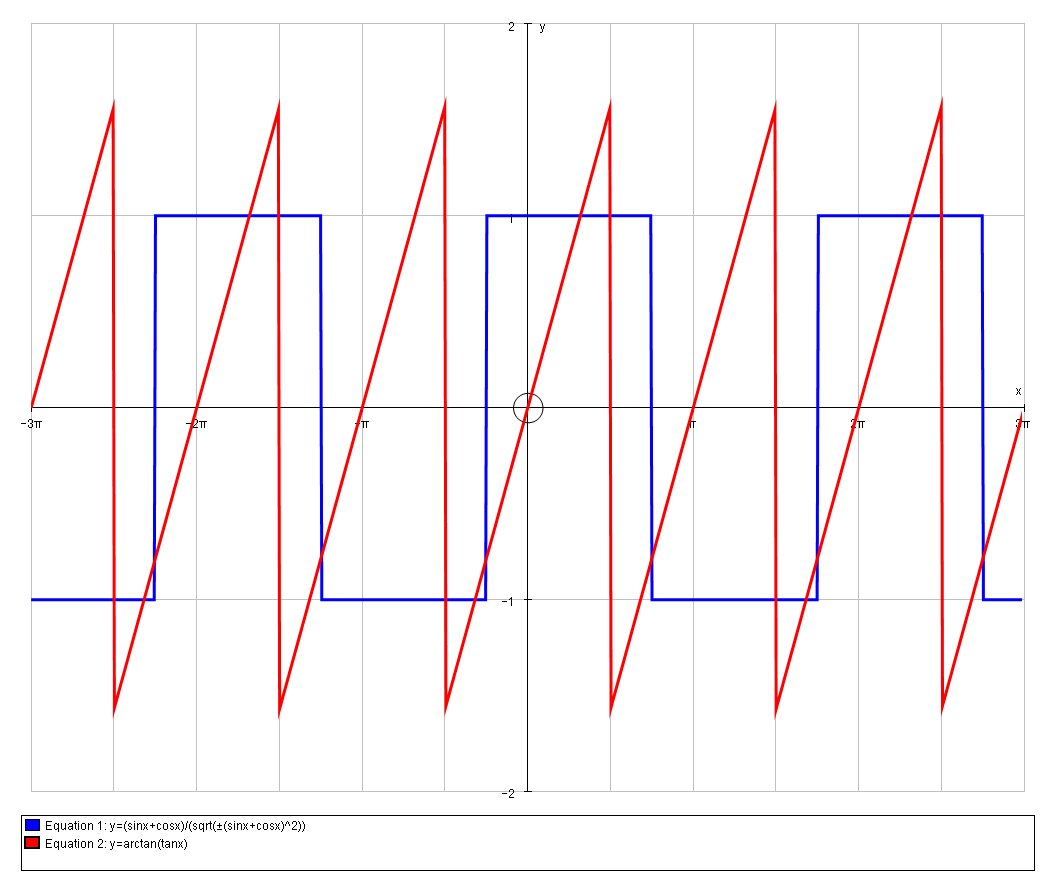
And we see that we get a periodic sawtooth function appropriate for the area under a square wave function.


