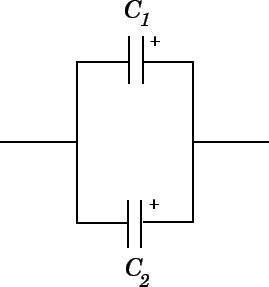
A 3.91 μF capacitor and a 7.41 μF capacitor are connected in series across a 12.0 V battery. What voltage would be required to charge a parallel combination of the same two capacitors to the same total energy?

Question

18600 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-08-02T16:54:29

#5.7"V"#

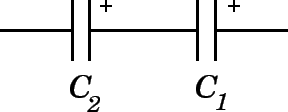
farside.ph.utexas.edu

The capacitance #C# of 2 capacitors in series like this is given by:

#1/C=1/C_(1)+1/C_2#

This can be rearranged to:

#C=(C_(1)C_(2))/(C_(1)+C_(2))#

#C=(3.91xx10^(-6)xx7.41xx10^(-6))/((3.91+7.41)xx10^(-6))#

#C=2.56xx10^(-6)"F"#

#=2.56mu"F"#

The energy of a capacitor is given by:

#E=1/2CV^(2)#

#E=1/2xx2.56xx10^(-6)xx12^(2)#

#E=1.84xx10^(-4)"J"#

For capacitors in parallel:

farside.ph.utexas.edu

#C=C_1+C_2#

#C= 3.91+7.41=11.32mu"F"#

#E=1/2CV^2#

#V^(2)=(2E)/(C)#

#=(2xx1.84xx10^(-4))/(11.32xx10^(-6))#

#V^(2)=32.5#

#V=5.7"V"#