Combination Capacitor Circuits

Key Questions

  • Question #dd1e3

    For capacitors in parallel:

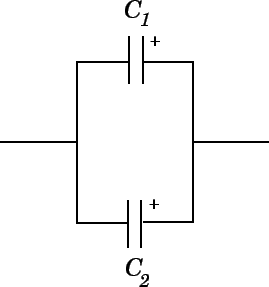
    farside.ph.utexas.edu

    The total capacitance #C_(TOT# is given by:

    #C_(TOT)=C_1+C_2#

    Since #C_(TOT)=Q/V# the total can be found from #Q=C_(TOT)V# where V is the voltage drop across the capacitors.

    For capacitors in series:

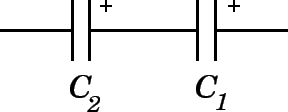
    farside.ph.utexas.edu

    #1/C_(TOT)=1/C_1+1/C_2#

    So #Q=C_(TOT)V#

    Michael · 1 · Jan 4 2015
  • What are some examples of combinations of capacitors?

    Series, parallel and combinations of series and parallel/

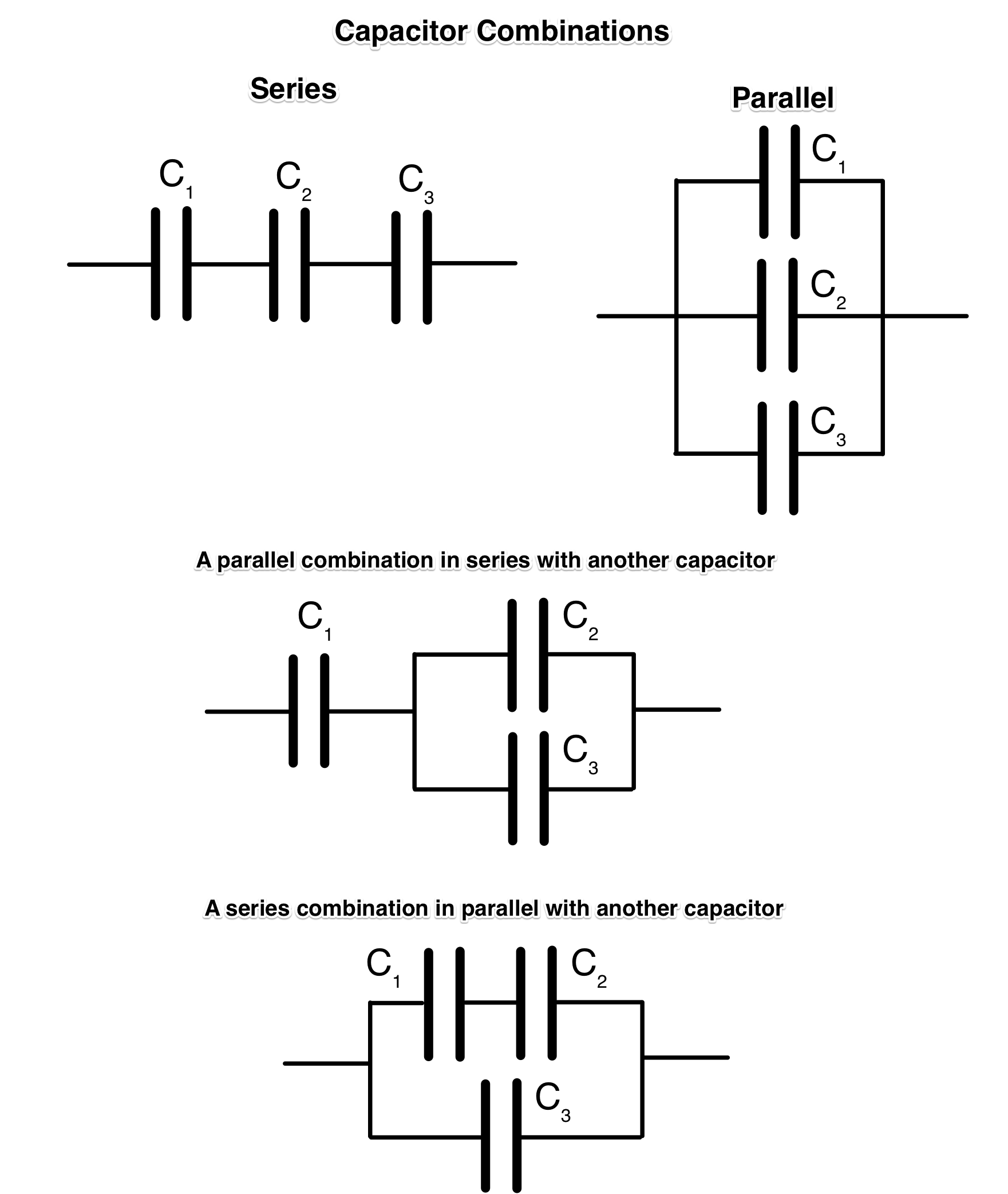
    enter image source here

    There are four examples of combinations in the diagram. The following points show how to calculate the total capacitance of each combination.
    1. Series
    The equivalent capacitance, C , of the combination is worked out as follows:

    #1/C=1/C_1+1/C_2+1/C_3#
    or
    #C=1/(1//C_1+1//C_2+1//C_3)#

    Total capacitance decreases in series.

    2. Parallel
    #C=C_1+C_2+C_3#

    Total capacitance increases in parallel.

    3. "Parallel in series"

    #1/C=1/C_1+1/(C_2+C_3)#

    4. "Series in parallel"

    #C=1/(1//C_1+1//C_2)+C_3#

    Example with numbers based on combination 4.

    #C_1=200muF#, #C_2=400muF#, #C_3=400 muF#

    #C=1/(1//(200*10^(-6))+1//(400*10^(-6)))+(400*10^(-6))#

    #⇒C=1/7500+400*10^-6=133*10^-6+400*10^-6#

    #C=533muF#

    Daniel W. · 1 · Dec 14 2014

Questions

Circuits