Question

A ball is tossed up from a tower `"50 m"` above the ground. If the ball has an initial velocity of `"30 m/s"`, how long will it take to hit the ground if `g = -"9.81 m/s"^2`. Help!?

Answer 1

Here's what I got.

Explanation:

The cool thing to consider here is the fact that you can break the motion of the ball into three parts

• from `"50 m"` above the ground to max height `->` going up
• from max height to `"50 m"` above the ground `->` going down
• from `"50 m"` above the ground `->` going down

So if you throw the ball from a height of `"50 m"` with an initial velocity of `"30 m s"^(-1)`, it will decelerate under the influence of gravity until it comes to a complete stop at the top of its trajectory, i.e. at maximum height, then accelerate under the influence of gravity until it reaches the ground.

So, if the velocity of the ball is equal to `"0 m s"^(-1)` at the top of its trajectory, you can say that you have

`"0 m s"^(-1) = v_0 - g * t_ "up from 50 m"`

which, in your case, is equal to

`"0 m s"^(-1) = "30 m s"^(-1) - "9.81 m s"^(-2) * t_ "up from 50 m"`

This means that the ball will reach the peak of its trajectory in

`t_ "up from 50 m" = (30 color(red)(cancel(color(black)("m"))) color(red)(cancel(color(black)("s"^(-1)))))/(9.81color(red)(cancel(color(black)("m"))) "s"^color(red)(cancel(color(black)(-2)))) = "3.06 s"`

Now, when the ball reaches `"50 m"` above the ground on its way down, its velocity will actually be equal to the initial velocity, only it will be pointed towards the ground.

This happens because the ball is in free fall from its maximum height, so the time it takes for the ball to reach `"50 m"` on its way down will be equal to the time it took for it to reach maximum height.

`"time up from 50 m to max height = time down from max height to 50 m"`

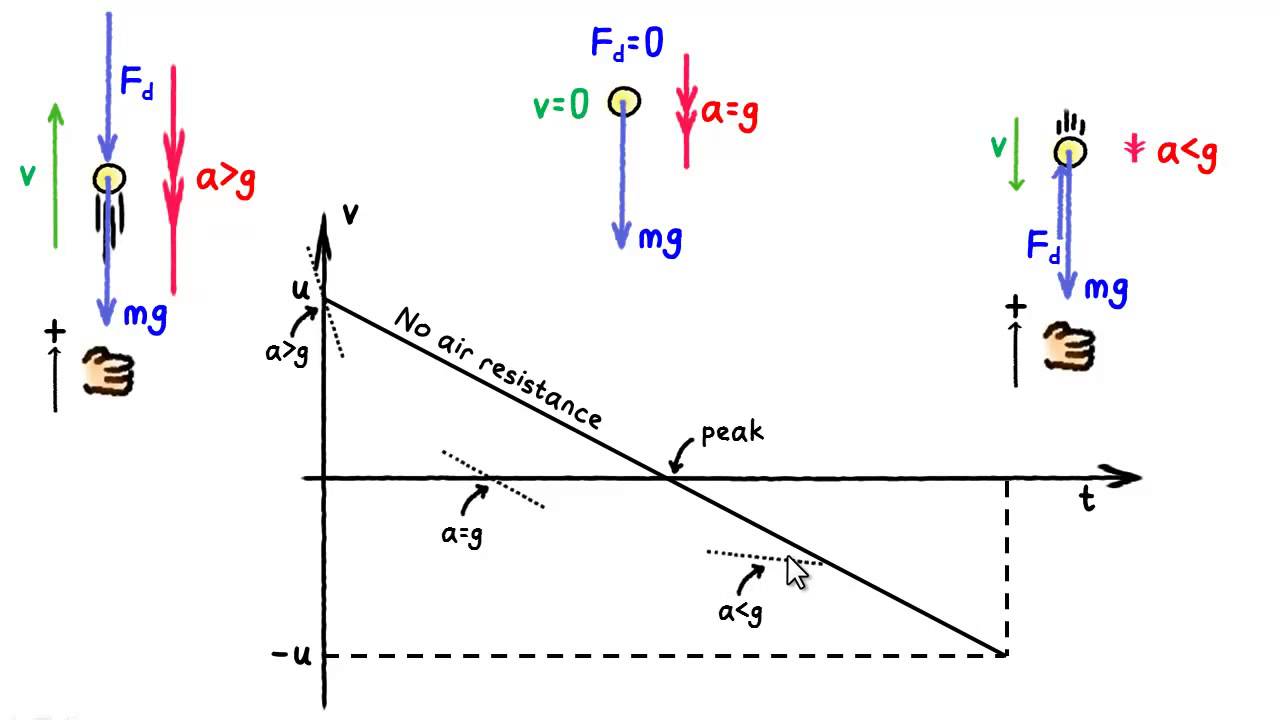
So

`t_"down to 50 m" = "3.06 s"`

So you know for a fact that when the ball reaches `"50 m"` above the ground going down, it will have a velocity of `"30 m s"^(-1)`.

This means that for the last portion of the movement, you can look consider a ball thrown from `"50 m"` with `"30 m s"^(-1)` pointed down.

You can find the impact velocity by using the equation

`v_f^2 = v_0^2 + 2 * g * h`

This will get you

`v_f = sqrt(("30 m s"^(-1))^2 + 2 * "9.8 m s"^(-2) * "50 m")`

`v_f = "43.37 m s"^(-1)`

This means that you have

`v_f = v_o + g * t_ "50 m to ground"`

which gets you

`t_"50 m to ground" = (43.37 color(red)(cancel(color(black)("m"))) color(red)(cancel(color(black)("s"^(-1)))) - 30 color(red)(cancel(color(black)("m"))) color(red)(cancel(color(black)("s"^(-1)))))/(9.81color(red)(cancel(color(black)("m"))) "s"^color(red)(cancel(color(black)(-2))))`

`t_"50 m to ground" = "1.36 s"`

Therefore, you can say that the total time needed for the ball to hit the ground is

`t_"total" = t_"up from 50 m" + t_ "down to 50 m" + t_ "50 m to ground"`

`t_ "total" = "3.06 s" + "3.06 s" + "1.36 s"`

`color(darkgreen)(ul(color(black)(t_"total" = "7.5 s")))`

I'll leave the answer rounded to two sig figs, but keep in mind that you only have one significant figure for your values.