PLEASE HELP WITH THIS PHYSICS QUESTION!!??
A ball thrown vertically upward with an initial speed of 2.8 from a window that is 3.6m above the ground. How long after the first ball is thrown should a second ball be simply dropped from the same window so that both balls hit the ground at the same?
A ball thrown vertically upward with an initial speed of 2.8 from a window that is 3.6m above the ground. How long after the first ball is thrown should a second ball be simply dropped from the same window so that both balls hit the ground at the same?
2 Answers
Explanation:
The first ball describes the path given by
At time
and both hit the ground at the same time.
Solving for
Attached a plot showing both paths.
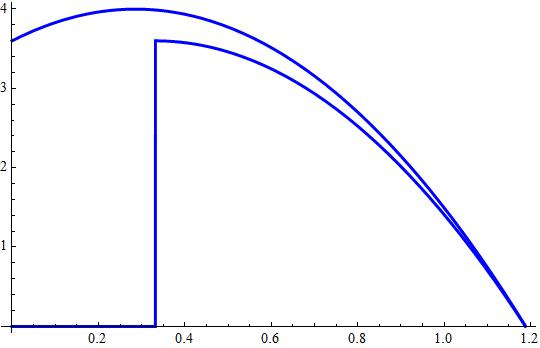
Explanation:
Time taken by the second ball to hit ground after it is just dropped is governed by the kinematic equation
Inserting given values and taking
Ignoring the negative root as time can not be negative we get
Time taken by the first ball to hit ground after it is thrown vertically up is also governed by the kinematic equation (1). However, in this case gravity is acting against the direction of motion and distance is also negative as ball hits the ground. We get
This quadratic equation can be solved using the formula
I used inbuilt graphics tool to find out the roots. Valid root for time is
If both balls are to hit ground together, second ball should be released after time

