A ball with a mass of # 5# #kg# is rolling at #4# #ms^-1# and elastically collides with a resting ball with a mass of #3# #kg#. What are the post-collision velocities of the balls?
2 Answers
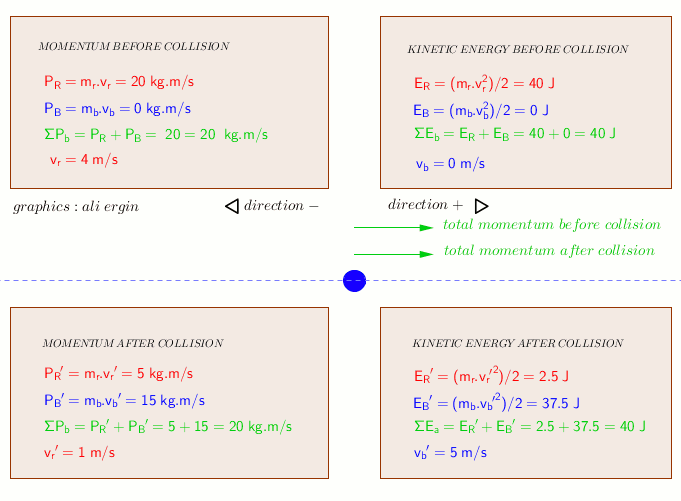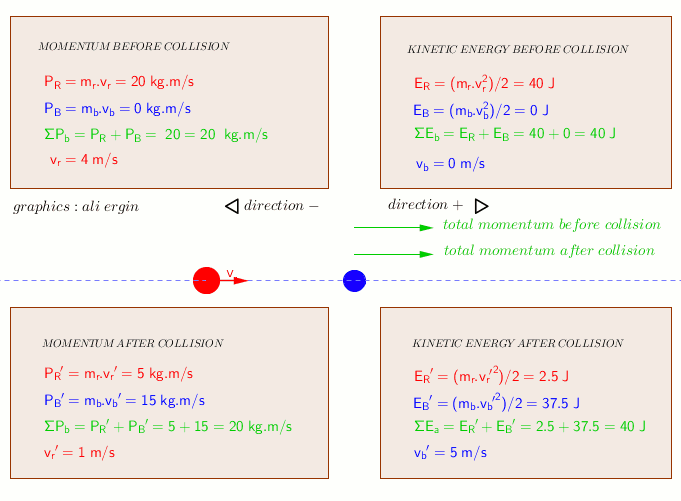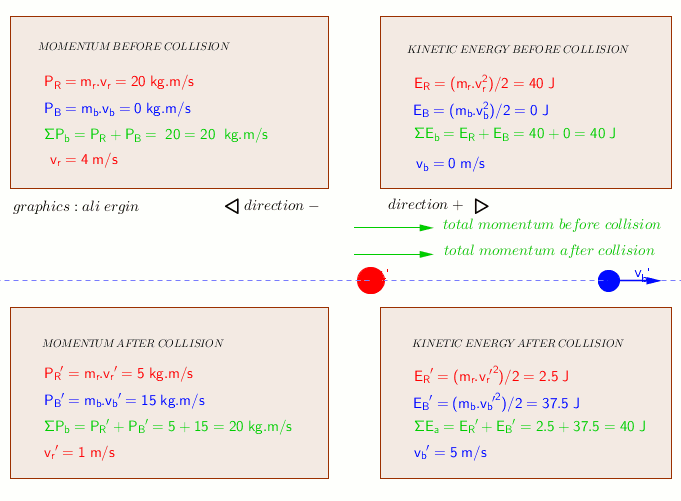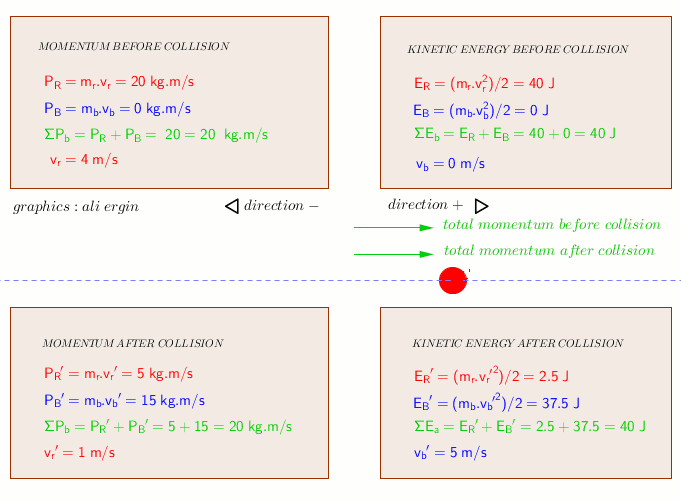
Momentum is always conserved, and the key word 'elastically' tells us that kinetic energy is also conserved. The calculation below shows how we determine the final velocities of the balls, which are
Explanation:
Momentum before the collision:
Kinetic energy before the collision:
(the stationary ball has a momentum of
The fact that momentum and kinetic energy are conserved mean that the total momentum after the collision will be
Call the
For momentum:
For kinetic energy:
We can substitute in the known masses to make these simpler:
To make it even a little neater, let's multiply equation B' by 2:
Rearranging equation A',
Substituting this value of
Expanding the square:
Subtract 80 from both sides and rearrange:
Multiplying through by 5 (I hate fractions):
Dividing through by
Substituting back into A':
We can substitute these values back into A and B to check them.
Explanation: