A box with an initial speed of #5# #ms^-1# is moving up a ramp. The ramp has a kinetic friction coefficient of #2/5 # and an incline of #pi /6 #. How far along the ramp will the box go?
1 Answer
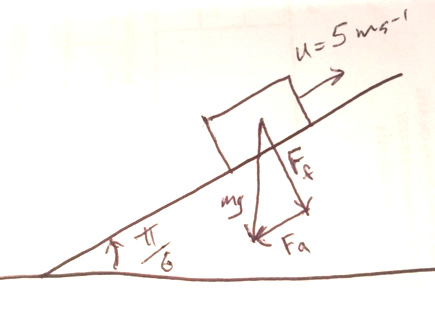
See below for the calculation of the acceleration, and the solution for the distance travelled up the slope is:
Explanation:
We might assume we need to know the mass of the box, but I suspect that it will cancel out and we won't need it.
We need to calculate the frictional force acting and the force parallel to the slope. Both of them will be acting to decelerate (slow) the box until its final velocity is
Remember that the angle is expressed in radians, so use the correct setting on your calculator.
See the diagram above. The forces are both supplied by the force of gravity on the box,
I've called the force perpendicular to the slope
(remember, we can leave
We know that
I've called the other component of the force, the one parallel to the slope,
The combined force acting to slow the object as it moves up the slope will be the sum of these two forces:
The acceleration will be given by Newton's Second Law,
(see, told you the
We will express it as a negative number, since the acceleration is in the opposite direction to the initial velocity.
We now need to calculate the distance the box moves:
Rearranging:
