A box with an initial speed of #6 m/s# is moving up a ramp. The ramp has a kinetic friction coefficient of #1/2 # and an incline of #(3 pi )/8 #. How far along the ramp will the box go?
1 Answer
Jun 10, 2016
I found
Explanation:
Consider the diagram:
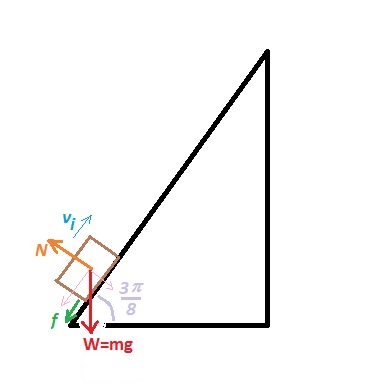
We can use Newton's Second Law:
Where:
along the horizontal (along the ramp):
along the vertical:
We also need to change
we can use kinematics and:
with
So we get:

