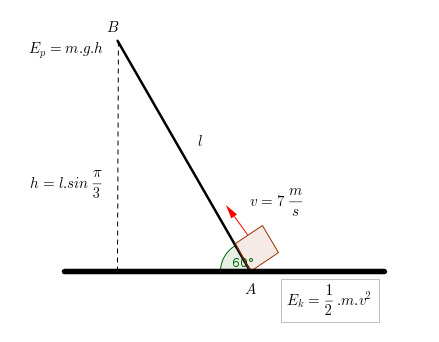
A box with an initial speed of #7 m/s# is moving up a ramp. The ramp has a kinetic friction coefficient of #1/3 # and an incline of #( pi )/3 #. How far along the ramp will the box go?

Question

1199 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-04-28T19:13:30

#l=2,41 " meters"#

enter image source here

#"total energy ":E_k=1/2*m*v^2" (at A)"#

#"energy changed heat due to friction :" W_f=mu* m*g*cos (pi/3)*l#

#"potential energy for the point of A :"E_p=m*g*h#

#"we can write the energy conservation equation as :"#

#E_k=E_p+W_f#

#1/2*m*v^2=m*g*h+mu*m*g*cos (pi/3)*l#

#"so ;"h=l.sin (pi/3)#

#1/2*cancel(m)*v^2=cancel(m)*g*l*sin(pi/3)+mu*cancel(m)*g*cos (pi/3)*l#

#1/2*v^2=g*l*0,87+1/3*g*0,5*l#

#v^2=g*l(2*0,87+(2*0,5)/3)#

#v=7 m/s#

#7^2=g*l(1,74+1/3)#

#49=g*l((5,22+1)/3)#

#49=g*l*2,07#

#g=9,81 m/s^2#

#49=9,81*l*2,07#

#49=20,31*l#

#l=2,41 " meters"#