A box with an initial speed of #8 m/s# is moving up a ramp. The ramp has a kinetic friction coefficient of #3/5 # and an incline of #pi /4 #. How far along the ramp will the box go?
1 Answer
Consider this scenario,
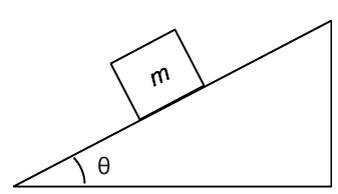
Moreover, assess the coordinate system as to be parallel with the incline. We are given this data,
We need three vectors, and resolve gravity into its components due to the preceding coordinate system. A vertical vector pointing down, (i) gravity, a vector pointing up perpendicular to the incline, (ii) normal force, and a vector pointing to the left, (iii)
Now, using Newton's second law, we resolve the gravity vector into its x and y components. (something like this, but friction is pointing left is well)

Recall,
Hence,
Furthermore, recall,
and assume the
Hence,
Not very far, the kinetic friction is very high!

