A box with an initial speed of #8 m/s# is moving up a ramp. The ramp has a kinetic friction coefficient of #3/4 # and an incline of #(5 pi )/12 #. How far along the ramp will the box go?

Question

1238 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-04-06T12:43:29

The distance is #=2.81m#

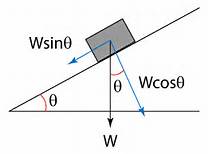
enter image source here

Solving in the direction of the plane #↗^+#

#mu_k=F_k/N#

#F_k=mu_kN#

#N=mgcostheta#

#F_k=mu_kmgcostheta#

The component of the weight is

#=mgsintheta#

Applying Newton' second Law

#-mu_kmgcostheta-mgsintheta=ma#

Therefore,

#a=-u_kgcostheta-gsintheta#

#=-3/4*g*cos(5/12pi)-g*sin(5/12pi)#

#=-11.4ms^-2#

The initial velocity is #u=8ms^-1#

We apply the equation of motion

#v^2=u^2+2as#

#0=64-2*11.4*s#

#s=64/(2*11.4)#

#=2.81m#