A bulb of resistance R=16 ohms is attached in series with an infinite resistor network with identical resistances r ohms. A 10 V battery drives current in the circuit. What should be the value of 'r' such that the bulb dissipates about 1 W of power?
Thank you!
Thank you!
1 Answer
Explanation:
Let
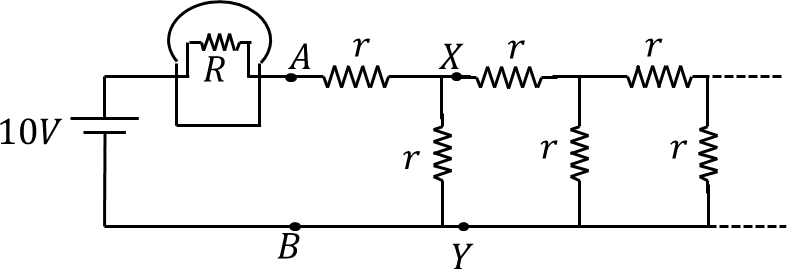
Total resistance seen by battery
Current in the bulb is given by the expression
Power dissipated in the bulb is
Inserting given values we get from (1)
Taking square root of both sides we get
To calculate
As there are infinite many resistors, there will still be infinite many resistors if we detach the first two resistors from the front of nodes
As such the network reduces to sum of two resistances 1. resistance
For infinite resistor network we have an equation
#R_e=r+(rxxR_e)/(r+R_e)#
#=>(R_e-r)=(rxxR_e)/(r+R_e)#
#=>(R_e-r)xx(r+R_e)=(rxxR_e)#
#=>(R_e^2-r^2)-(rxxR_e)=0#
Using (3) we get
#(24^2-r^2)-24r=0#
#=>r^2 +24r-24^2=0#
Solving the quadratic and choosing positive root as resistance can not be negative
-.-.-.-.-.-.-.
Quadratic equation can also be solved using inbuilt graphic utility

