Question

A capacitor is formed by two square metal plates of edge a, separated by a distance d, Dielectrics of dielectric constants `K_1` and `K_2` are filled in the gap as shown in figure. Find the capacitance.?

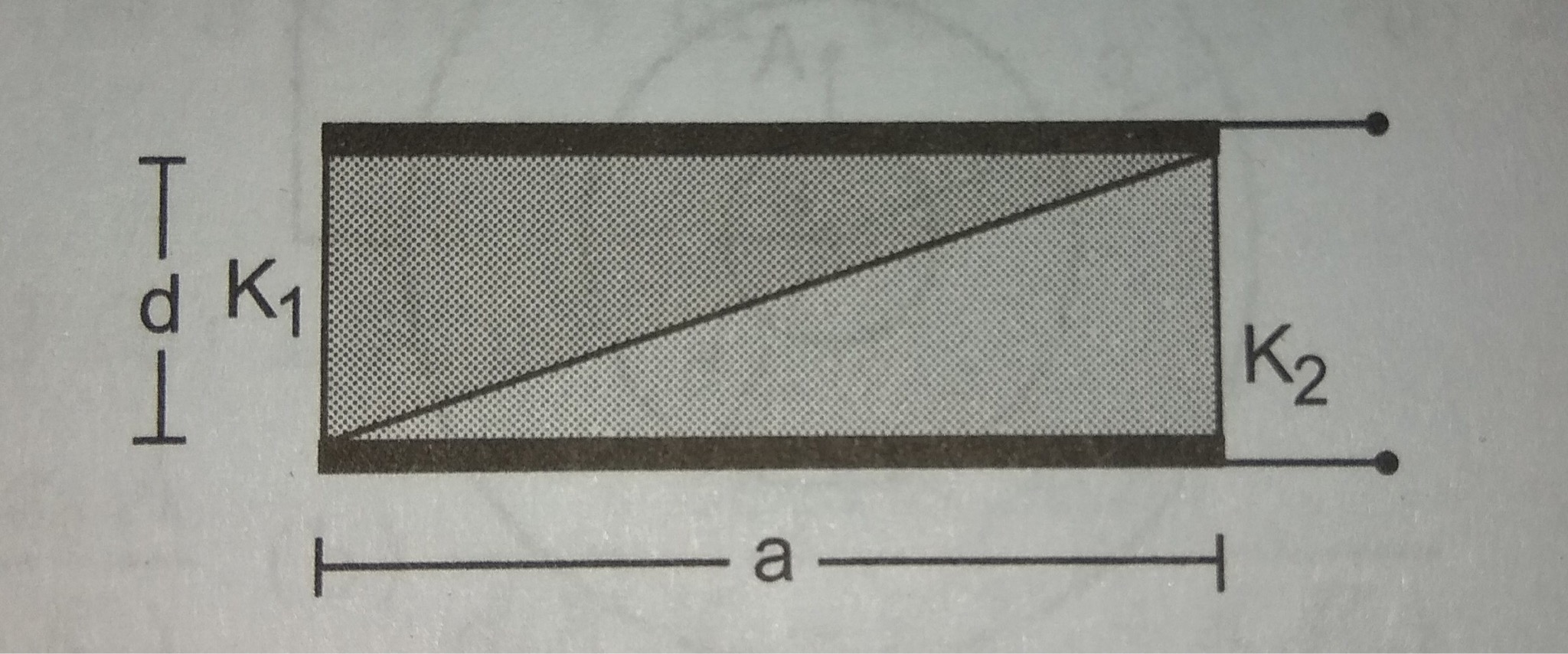
Answer: `C = (ε_0K_1K_2a^2ln[K_1/K_2])/((K_1 - K_2)d)`

Answer 1

Consider an infinitesimal strip of of capacitor of thickness `dx` at a distance `x` as shown. Keeping in view the position of terminlas we see that the infinitesimal capacitors so formed are connected in series.
Plate separation for lower part is `xtanalpha` whereas for the upper part it is `(d-xtanalpha)`.
We know that equivalent capacitance of capacitors connected in series is given by the expression

`1/(dC_(eq))=1/(dC_(K_1))+1/(dC_(K_2))`

Inserting value for Parallel-plate capacitor of plate area `A` and plate separation `t` as `C=epsilon_0A/t`, we get

`1/(dC_(eq))=(d-xtanalpha)/(K_1epsilon_0(adx))+(xtanalpha)/(K_2epsilon_0(adx))`
`=>1/(dC_(eq))=1/(epsilon_0adx)[(d-xtanalpha)/(K_1)+(xtanalpha)/(K_2)]`
`=>dC_(eq)=(epsilon_0adx)/[(d-xtanalpha)/(K_1)+(xtanalpha)/(K_2)]`
`=>dC_(eq)=(K_1K_2epsilon_0adx)/[K_2(d-xtanalpha)+K_1(xtanalpha)]`
`=>dC_(eq)=(K_1K_2epsilon_0adx)/[K_2d+(K_1-K_2)(tanalpha)x]`

Integrating both sides with respect to respective variables from `C=0toC_(eq) and x=0toa` we get

`C_(eq)=(K_1K_2epsilon_0a)int_0^a(dx)/[K_2d+(K_1-K_2)(tanalpha)x]`

Using the following integral we get

`int(dx)/(b*x+c)=ln(abs(b*x+c))/b`

`C_(eq)=(K_1K_2epsilon_0a)/((K_1-K_2)(tanalpha))[ln(|K_2d+(K_1-K_2)(tanalpha)x|)]_0^a`

`=>C_(eq)=(K_1K_2epsilon_0a)/((K_1-K_2)(tanalpha))[ln(|K_2d+(K_1-K_2)(tanalpha)a|)-(ln(|K_2d|)]`

Inserting `tanalpha=d/a`, we get
`C_(eq)=(K_1K_2epsilon_0a^2)/((K_1-K_2)d)[ln(|K_2d+(K_1-K_2)d|)-ln(|K_2d|)]`

Simplifying

`C_(eq)=(K_1K_2epsilon_0a^2)/((K_1-K_2)d)[ln((K_1d)-(ln(K_2d)]`
`=>C_(eq)=(K_1K_2epsilon_0a^2)/((K_1-K_2)d)ln(K_1/K_2)`