A chemical reaction occurring in a cylinder equipped with a moveable piston produces 0.58 mol of a gaseous product. If the cylinder contained 0.11 mol of gas before the reaction and had an initial volume of 2.1L, what was its volume after the reaction?
1 Answer
The new volume of the cylinder will be equal to 13 L.
When no mention of pressure or temperature is made, you can assume that they are kept constant. This means that you can use Avogadro's Law to determine what the new volume of the cylinder will be.
According to Avogadro's Law, the volume of a gas is directly proportional to the number of moles of gas present, when temperature and pressure are kept constant.
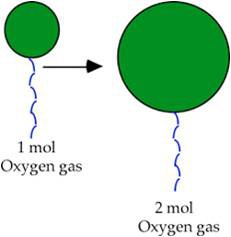
In other words, the bigger the number of moles of gas present, the bigger the volume. Think about blowing up a balloon. The more you put into it, the bigger its volume gets.
Mathematically, this relationship is expressed like this
You know that your reaction produces 0.58 moles of gas, and that 0.11 moles of gas were already in the cylinder. This means that the total number of moles present in the cylinder after the reaction is completed will be
Use the above equation to solve for
Rounded to two sig figs, the answer will be

