A circle has a chord that goes from #( 3 pi)/2 # to #(7 pi) / 4 # radians on the circle. If the area of the circle is #99 pi #, what is the length of the chord?
1 Answer
7.62 units
Explanation:
First, use a unit circle to determine the end points of the chord on the circle.
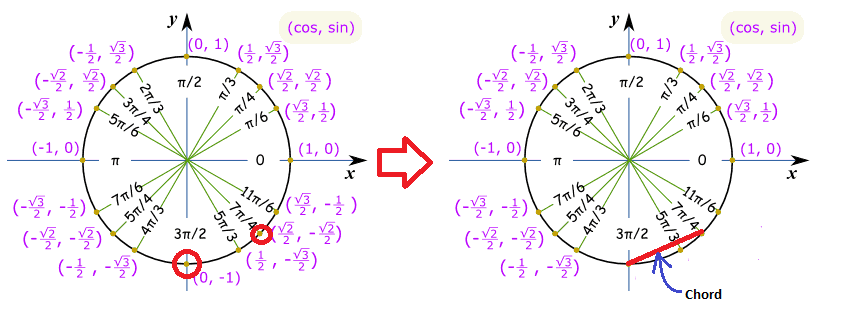
If each endpoint on the chord is connected to the center of the circle, an isosceles triangle is formed whose congruent sides each have a length of
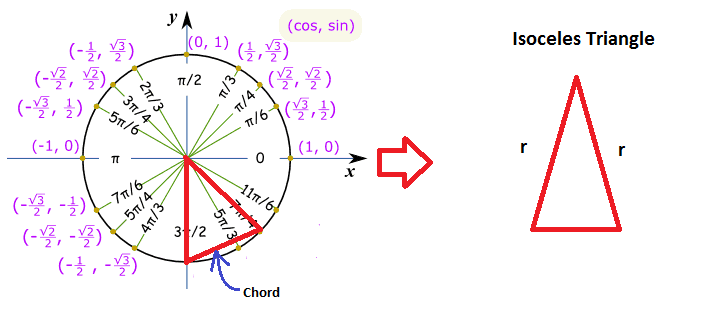
The angle between the two equivalent sides of the triangle is equal to the difference between the angles given in the problem:
Finally, the law of cosines can be used to determine an equation for the length of the chord:
Since both
The problem states that the area of the circle is
Plug this value into the equation for the chord:
Note: Since the units of length are not provided, just use "units."

