Question

A circle has a chord that goes from `( pi)/8` to `(4 pi) / 3` radians on the circle. If the area of the circle is `64 pi`, what is the length of the chord?

Answer 1

`c=sqrt{(8cos(pi/8)+4)^2+(8sin(pi/8)+4sqrt3)^2}`
`c approx 15.15088`

Explanation:

Radius:
Area`=64pi`
`pir^2=64pi`
`r^2=64`
`r=8`

Chord length:
The first angle, `pi/8`, is in quadrant I, and the second angle, `(4pi)/3`, is in quadrant III. Imagine a right triangle where the hypotenuse is the chord from polar coordinates `(8,pi/8)` to `(8,(4pi)/3)`. The horizontal and vertical distances can be found by adding the absolute values of the cosine and sine values, respectively.

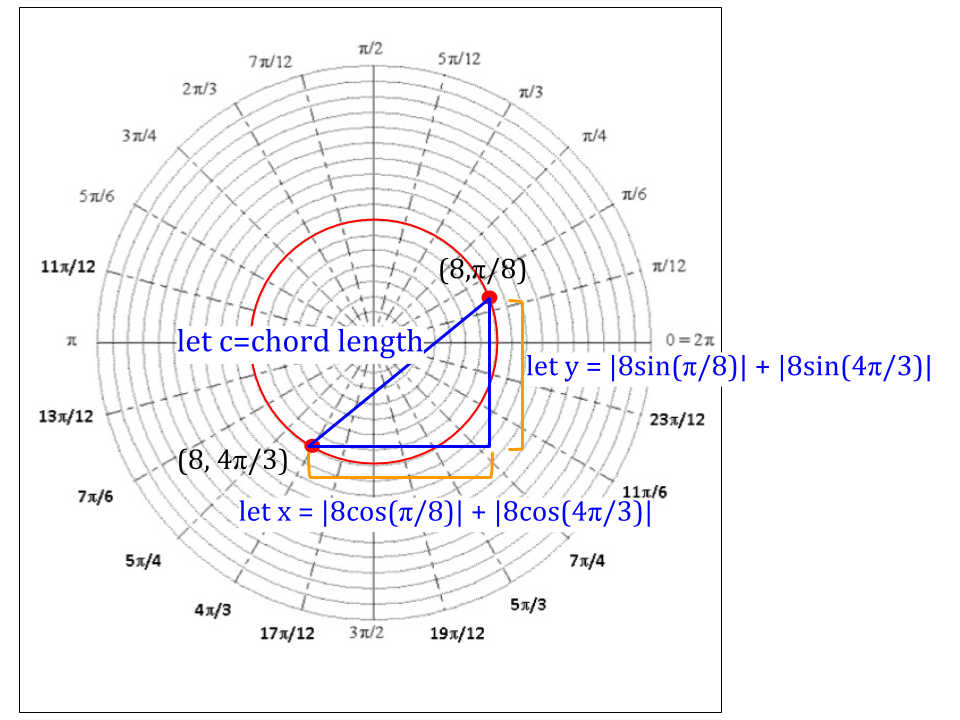
(Drawing not to scale)

To solve for chord length:
`x^2+y^2=c^2" (Pythagorean theorem)"`

Substitute in values for x and y (shown in drawing above):
`c^2 = [|8cos(pi/8)|+|8cos((4pi)/3)|]^2+[|8sin(pi/8)|+|8sin((4pi)/3)|]^2`

Simplify (get rid of absolute values by determining their sign)
`c^2=[8cos(pi/8)-8cos((4pi)/3)]^2+[8sin(pi/8)-8sin((4pi)/3)]^2`

`c^2=[8cos(pi/8)-8(-1/2)]^2+[8sin(pi/8)-8(-sqrt3/2)]^2`

`c^2=(8cos(pi/8)+4)^2+(8sin(pi/8)+4sqrt3)^2`

`c=sqrt{(8cos(pi/8)+4)^2+(8sin(pi/8)+4sqrt3)^2}`

`c approx 15.15088`

This answer appears correct because if the radius is 8, then the diameter is 16, and this given chord is just less than 16 because it is not the diameter.