Question

A conical paper cup is 10 cm tall with a radius of 30 cm. The cup is being filled with water so that the water level rises at a rate of 2 cm/sec. At what rate is water being poured into the cup when the water level is 9 cm?

Answer 1

Rate `= 1458pi \ cm^3s^-1`
`\ \ \ \ \ \ \ = 4580.44 \ cm^3s^-1 \ \ (2dp)`

Explanation:

Let us set up the following variables:

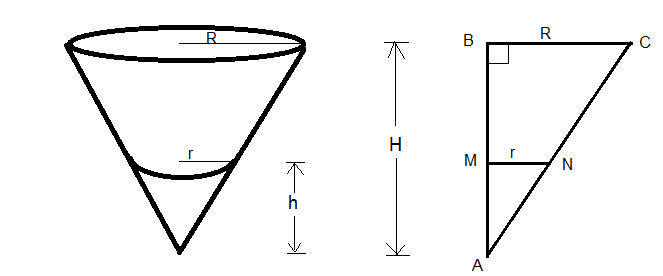
`{(R, "Radius of conical cup (cm)",=30 \ cm), (H, "Height of the conical cup (cm)",=10 \ cm), (t, "time", "(s)"), (h, "Height of water in cup at time t","(cm)"), (r, "Radius of water at time t","(cm)" ), (V, "Volume of water at time t", "(cm"^3")") :}`

Our aim is to find `(dV)/dt` when `h=9` and we are given `(dh)/dt=2`

By similar triangles we have

`r:h = R:H`

`:. r/h=30/10 => r = 3h`

The volume of a cone is `1/3pir^2h`, So:

`V = 1/3 pi r^2 h`
`\ \ \ = 1/3 pi (3h)^2 h`
`\ \ \ = 1/3 pi 9h^2 h`
`\ \ \ = 3pi h^3`

Differentiating wrt `h` we get:

`(dV)/(dh) = 9pih^2`

And Applying the chain rule we have:

`(dV)/(dt) = (dV)/(dh) * (dh)/(dt)`
`\ \ \ \ \ \ \= 9pih^2 * 2`
`\ \ \ \ \ \ \= 18pih^2`

And so when h=9 we have:

`[ (dV)/(dt) ]_(h=9) = 18pi(9^2) = 1458pi \ cm^3s^-1`