A gas with a volume of 4.0 L at 90.0 kPa expands until the pressure drops to 20.0 kPa. What is its new volume if the temperature doesn't change?
1 Answer
Explanation:
Before doing any calculations, try to predict what you expect to see happen to the volume of the sample.
The problem tells you that the temperature of the gas remains unchanged. No mention is made about the number of moles of gas present in the sample, which means that you can assume it to be constant as well.
As you know, temperature is actually a measure of the average kinetic energy of the gas molecules. Gas pressure is a result of the frequency and intensity of the collisions that take place between the gas molecules and the walls of the container.
If a pressure of
Think about it like this - the average kinetic energy of the gas molecules remains unchanged, which means that in order to produce a lower pressure they must hit the walls of the container less often.
The molecules are moving with the same average kinetic energy, which is why they must hit the walls of the container less often.
This can only be achieved by an increase in volume.
So, when temperature and number of moles are kept constant, pressure and volume have an inverse relationship - this is known as Boyle's Law.
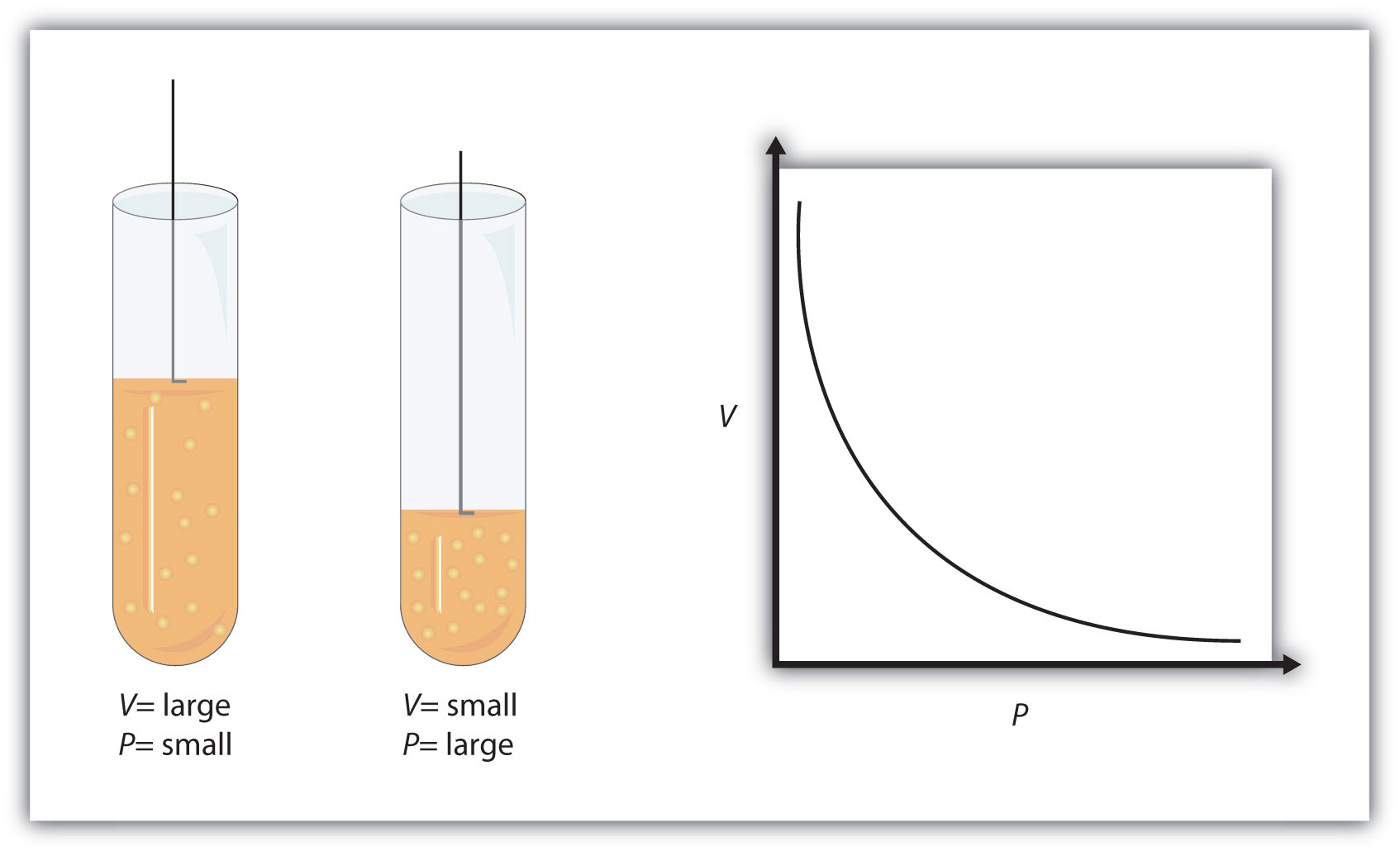
When pressure increases, volume decreases, and when pressure decreases, volume increases.
This means that you can expect the volume of the gas to increase.
Mathematically, you can write this as
#color(blue)(P_1V_1 = P_2V_2)" "# , where
Rearrange and solve for
#V_2 = P_1/P_2 * V_1#
#V_2 = (90.0 color(red)(cancel(color(black)("kPa"))))/(20.0color(red)(cancel(color(black)("kPa")))) * "4.0 L" = color(green)("18 L")#
As predicted, the volume of the gas increased as a result of the decrease in pressure.

